Data-Structure7

Before：新学期第一篇DS！写于物理学实验绪论课上😋

Data Structure 7 队列

队列的定义

队列是一种特殊的线性表，插入限定在表的一端，删除限定在表的另一端；允许进行插入的一端成为队尾，允许进行删除的一端称为队头；位于队头的元素称为队头元素，位于队尾的元素称为队尾元素。因为这一性质，队列也被称为FIFO表（先进先出）。

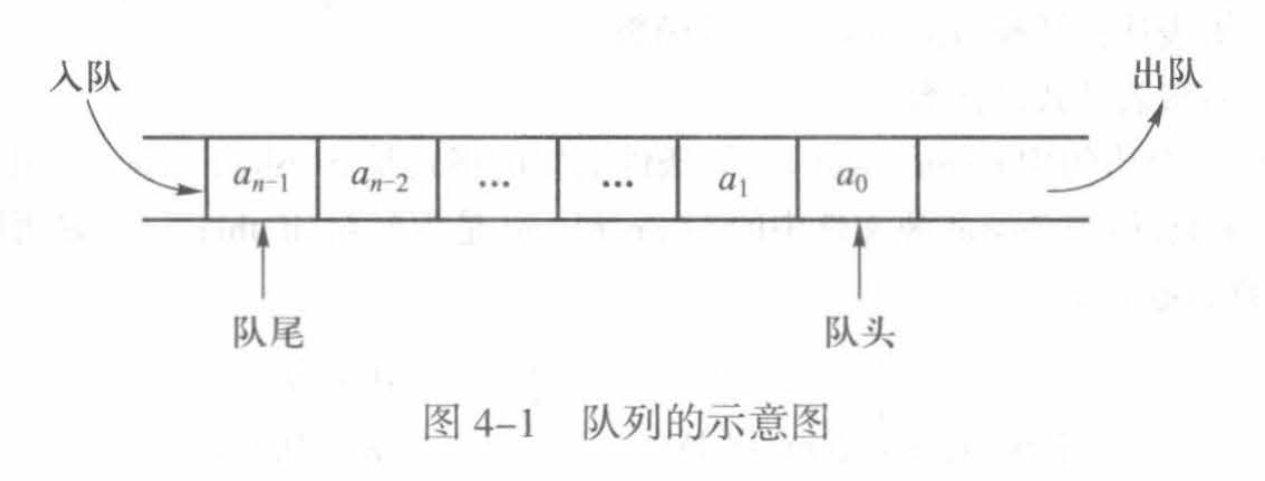
队列的基本操作有如下5种：

• 创建一个队列create()
• 入队enQueue(x)：将x插入队尾
• 出队deQueue()：删除队头元素
• 读队头元素getHead()
• 判空isEmpty()

下面是队列的抽象类定义：

template<class elemType>
class queue{
    public:
        virtual void enQueue(const elemType& x) = 0;
        virtual elemType deQueue() = 0;
        virtual elemType getHead() const = 0;
        virtual ~queue();
        virtual bool isEmpty() const = 0;
};

顺序队列的存储实现 用一维数组实现

1.队头位置固定
如下图所示：

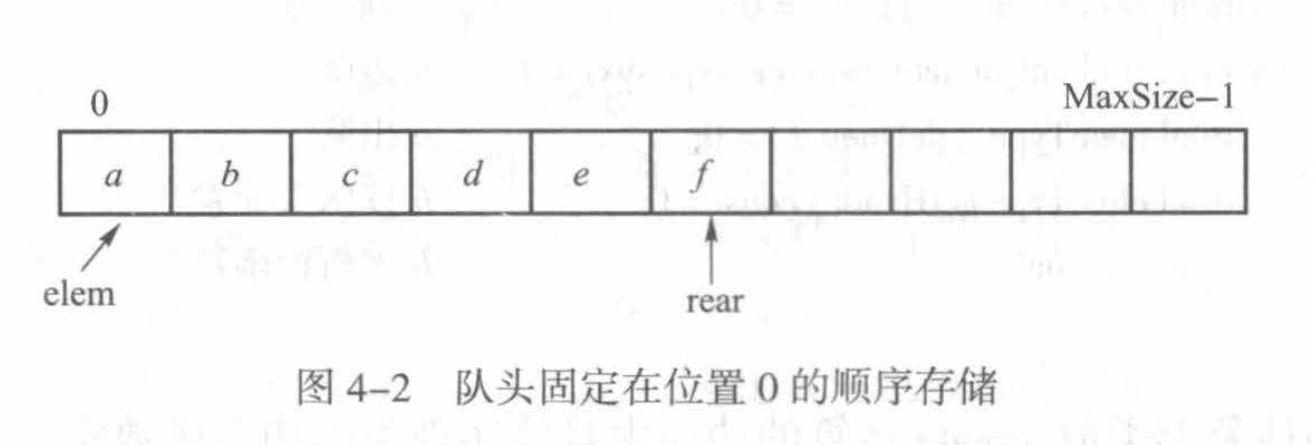
入队、读取队头元素、判空操作的复杂度均为O(1)，而入队操作的复杂度为O(N)，其实现方式类似于vector类的实现，故在这里不做具体实现
2.队头位置不固定的顺序实现
一旦入队后，存储位置保持不变，而队头位置在变化，只需增加一个变量front，用于存储队头位置，这样一来所有操作的复杂度均为O(1)
如下图所示：

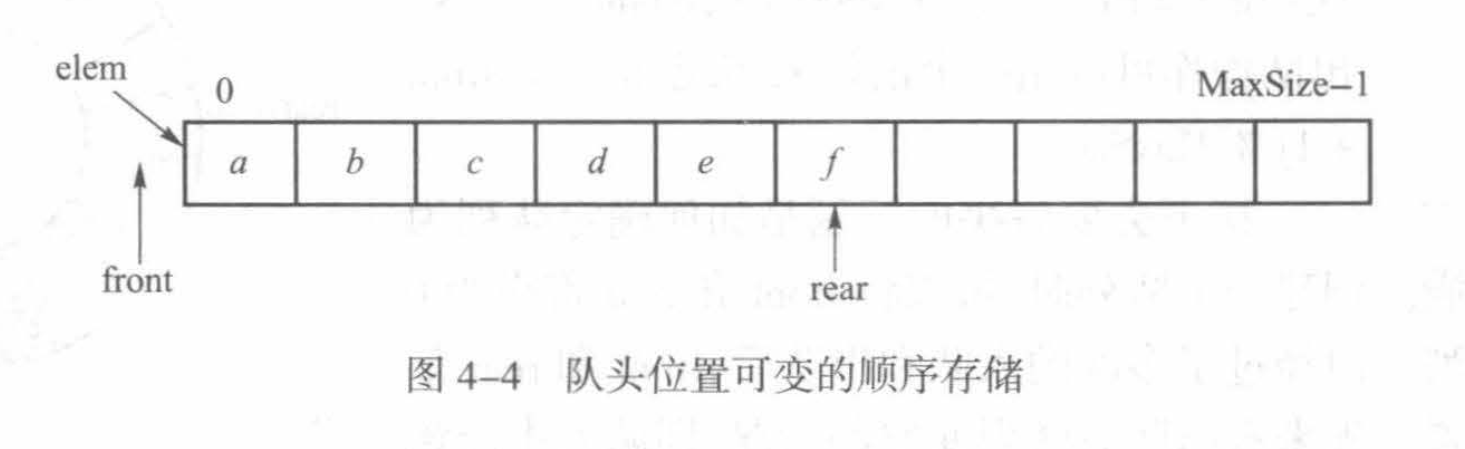
但是这种做法的弊端在于空间很快会被用完，空间利用率低，于是我们有了：
3.循环队列 最常用方案
我们可以将数列看作是首尾相连的，利用前面的空间，这样每次出队操作，有front = (front + 1)%MaxSize;
如下图所示：

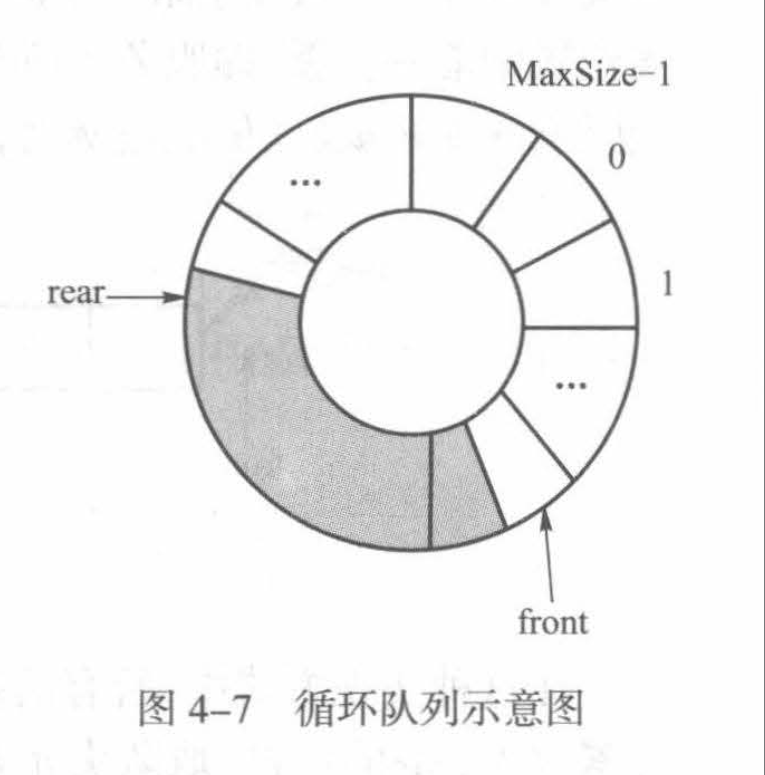
但是这会带来一个问题，就是队空和队满是，均有front == rear，两种情况无法区分。这时候我们可以联想在链表实现时我们构建的head结点，不存储元素。同样这种思想可以应用在这里，我们可以牺牲一个空间单元，规定front指向的单元不能存储元素，作为服务台，这样一来，队满的条件为：
(rear + 1)%MaxSize == front
队伍为空的条件为：
rear == front
下面给出循环队列的定义：

template<class elemType>
class seqQueue: public queue<elemType>{
    private:
        elemType *elem;
        int front,rear;
        int MaxSize;
        void doubleSpace();
    public:
        seqQueue(int size = 10);
        ~seqQueue();
        void enQueue(const elemType& x);
        elemType deQueue();
        elemType getHead() const;
        bool isEmpty() const;
};

循环队列的具体实现

template<class elemType>
seqQueue<elemType>::seqQueue(int size){
    elem = new elemType[size];
    MaxSize = size;
    front = 0;
    rear = 0;
}

template<class elemType>
seqQueue<elemType>::~seqQueue(){
    delete []elem;
}

template<class elemType>
void seqQueue<elemType>::enQueue(const elemType& x){
    if((rear + 1)%MaxSize == front){
        // 队伍已满
        doubleSpace(); //扩大空间
    }
    rear = (rear + 1)%MaxSize;
    elem[rear] = x;
}

template<class elemType>
elemType seqQueue<elemType>::deQueue(){
    if(!isEmpty()){
        front = (front + 1)%MaxSize;
        return elem[front];
    }
}

template<class elemType>
elemType seqQueue<elemType>::getHead() const{
    return elem[(front + 1)%MaxSize];
}

template<class elemType>
bool seqQueue<elemType>::isEmpty() const{
    return front == rear;
}

template<class elemType>
void seqQueue<elemType>::doubleSpace(){
    elemType *tmp = elem;
    elem = new elemType[2 * MaxSize];
    for(int i = 1;i <= MaxSize; i ++){
        elem[i] = tmp[(front + i)%MaxSize];
    }
    delete []tmp;
    front = 0;
    rear = MaxSize;
    MaxSize *= 2;
}

队列的链接实现

和上一章节讨论的栈的链接实现类似，链接队列同样用单链表实现，将单链表的表头作为队头，表尾作为队尾（出于时间复杂度均控制在O(1)的考虑），下面是链接队列的示意图：

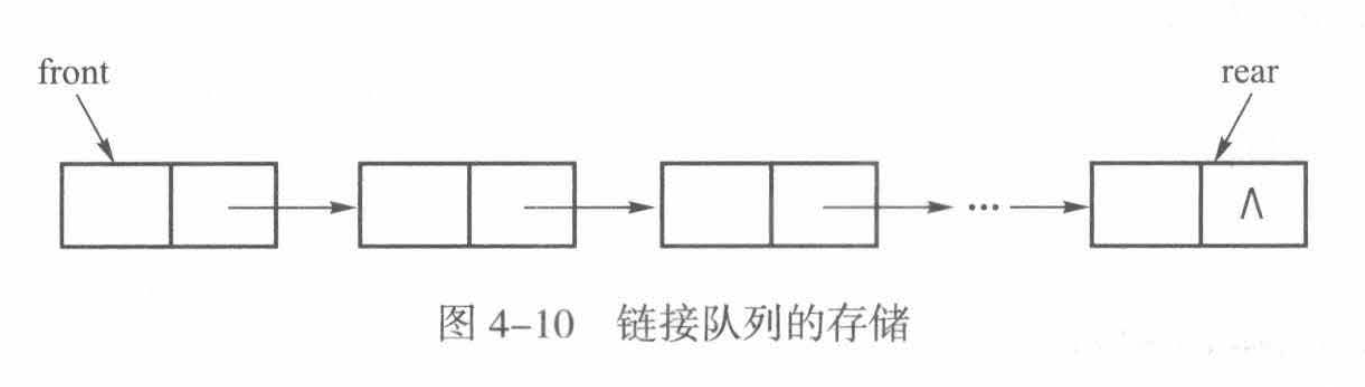
类似地，给出链接队列的定义：

template<class elemType>
class linkQueue: public queue<elemType>{
    private:
        struct Node{
            elem data;
            Node *next;
            Node(const elemType& x,node *N = nullptr){
                data = x;
                next = N;
            }
            Node(){
                next = nullptr;
            }
            ~Node(){}
        };
        node *front;
        node *rear;
    public:
        linkQueue();
        ~linkQueue();
        void enQueue(const elemType& x);
        elemType deQueue();
        elemType getHead() const;
        bool isEmpty() const;
};

下面是具体的链接队列实现：

template<class elemType>
linkQueue<elemType>::linkQueue(){
    front = nullptr;
    rear = nullptr;
}

template<class elemType>
linkQueue<elemType>::~linkQueue(){
    Node *tmp;
    while(front != nullptr){
        tmp = front;
        front = front -> next;
        delete tmp;
    }
}

template<class elemType>
void linkQueue<elemType>::enQueue(const elemType& x){
    if(rear == nullptr){
        front = new node(x);
        rear =  front;
    }else{
        rear -> next =  new node(x);
        rear = rear -> next;
    }
}

template<class elemType>
elemType linkQueue<elemType>::deQueue(){
    Node *p = front;
    front = front -> next;
    if(front == nullptr){
        rear = nullptr;
    }
    elemType tmp = p -> data;
    delete p;
    return tmp;
}

template<class elemType>
elemType linkQueue<elemType>::getHead() const{
    return front -> data; 
}

template<class elemType>
bool linkQueue<elemType>::isEmpty() const{
    return front == nullptr;
}

STL中的队列

与栈类似，STL中的队列也是一个容器适配器，借助于list或deque实现。所以同栈一样，在使用stl::queue时，需要指明2个参数，第一个为队列元素类型，第二个为借助的底层容器，若不指明则默认为deque
这里是第二次出现deque这个容器了，那么就让我们来了解一下这个似乎我们不常听闻的底层容器吧😄
⭐deque是一个双向队列（double-ended queue），可以在队列的两端进行元素的插入和删除操作。deque是C++STL（标准模板库）中的一种容器，可以用于存储各种类型的元素。特点是可以在队列的两端进行元素的操作，并且可以高效地在队列的任意位置进行元素的插入和删除操作。
其成员函数有如下这些：

push_back()//在队列的尾部插入元素。
emplace_front()//与push_front()的作用一样 
push_front()//在队列的头部插入元素。
emplace_back()//与push_back()的作用一样 
pop_back()//删除队列尾部的元素。
pop_front()//删除队列头部的元素。
back()//返回队列尾部元素的引用。
front()//返回队列头部元素的引用。
clear()//清空队列中的所有元素。
empty()//判断队列是否为空。
size()//返回队列中元素的个数。
begin()//返回头位置的迭代器
end()//返回尾+1位置的迭代器
rbegin()//返回逆头位置的迭代器 
rend()//返回逆尾-1位置的迭代器 
insert()//在指定位置插入元素 
erase()//在指定位置删除元素 

Reference

CSDN：https://blog.csdn.net/H1727548/article/details/130959610

End

关于队列的应用，后续会结合上机课内容，在算法部分另开一章进行解释