Data-Structure9
Before:这一章,我们要进入一种新的数据结构类型——树🌲🌳🌴🎄。lz早就听闻各种神奇的树(二叉树、平衡树、红黑树、线段树、B树、B+树…)😇😭😥,今天中午和学长吃饭得知他红黑树调了1个月找不出bug只好重构的事迹,已经开始害怕了😰咱们还是快开始吧!
Data Structure 9 树
为了满足一下某人的好奇心,决定先贴一张树的归纳总结的图,作为开端(自己宠自己)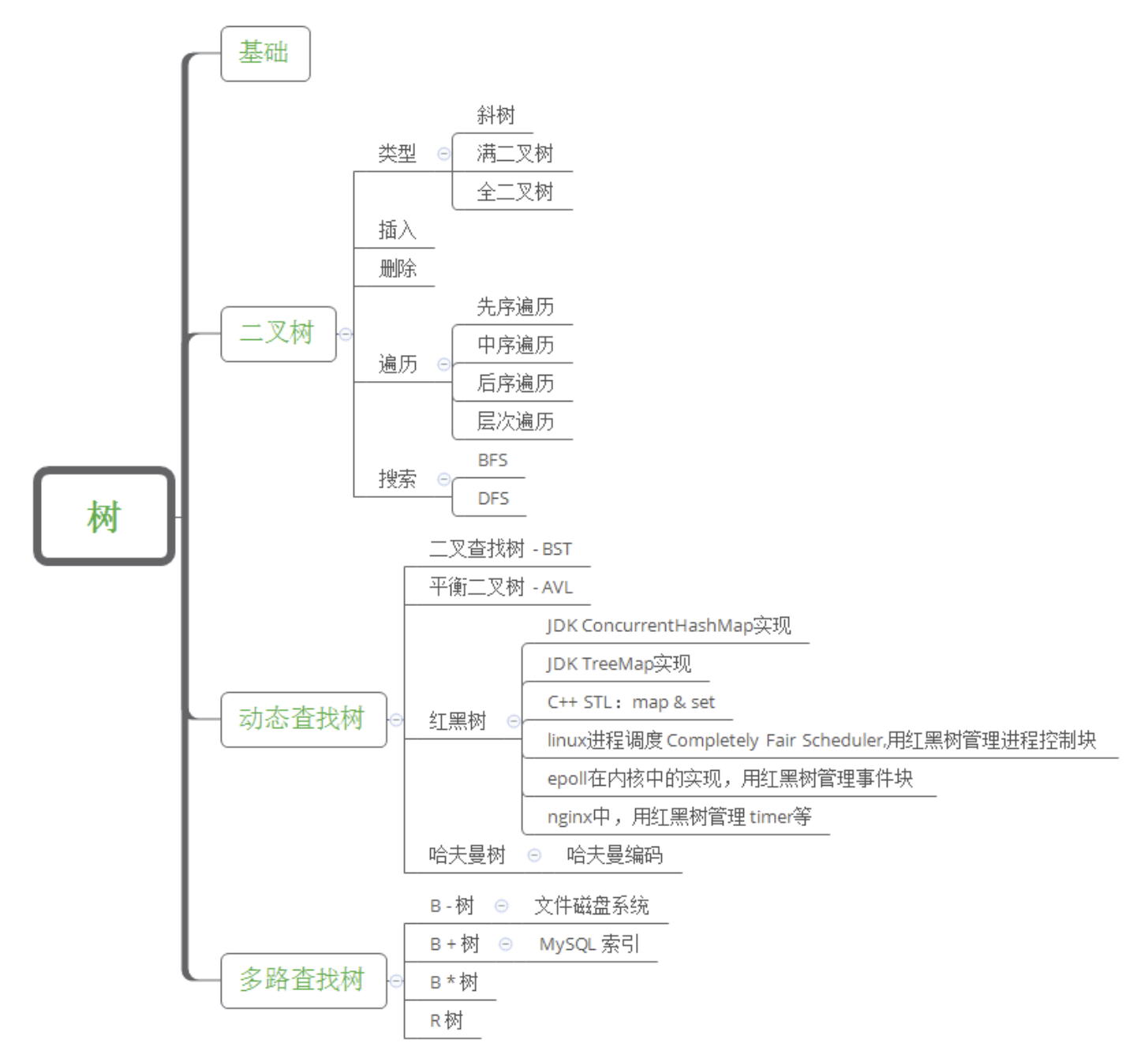
树的定义
首先,回顾一下树状结构的特点:只有一个直接前驱(除根结点外),但可以有多个直接后继。
树的递归定义:有n个结点的有限集合,或者是空集。拥有1个根结点,其余结点可分成m个互不相交的集合,这些集合本质上也是树,称作根节点的子树。
下面是树的一些基本术语:
- 根节点 叶节点(没有直接后继的结点) 内部结点(除根叶结点外)
- 结点的度(一个结点的直接后继数目) 树的度(所有结点的度的最大值)
- 子结点(结点的直接后继结点) 父结点(结点的直接前驱) 祖先节点(每个结点通向根结点的唯一路径上的所有结点) 子孙结点(该结点所有子树中的全部结点)
- 兄弟结点(同一个结点的子结点互为兄弟结点)
- 结点层次(相当于家谱中的第几代) 树的高度(结点的最大层次) 结点高度(以该结点为根的子树高度)
- 有序树(把树中每个结点的子树看成自左向右有序的)
- 森林(M棵互不相交的树的集合)
树的基本运算
(1)create() 创建空树
(2)clear() 清除树中所有结点
(3)isEmpty() 判别空树
(4)root() 找到根结点的值
(5)parent(x) 找到结点x的父结点值
(6)child(x,i) 找结点x的第i个子结点值
(7)remove(x,i) 删除结点i的第i棵子树
(8)traverse() 访问树上每一个结点
还是老样子,给出树的抽象类:
1 | |
二叉树 binary tree
放在第一个,那自然是因为它《简单且应用广泛》
二叉树是结点的有限集合,它或者为空,或者由一个根结点及两棵互不相交的左右子树构成,而其左、右子树又都是二叉树。注意:二叉树是有序树,必须严格区分左右子树。即使只有一棵子树,也要说明它是左子树还是右子树。
二叉树有5种基本形态: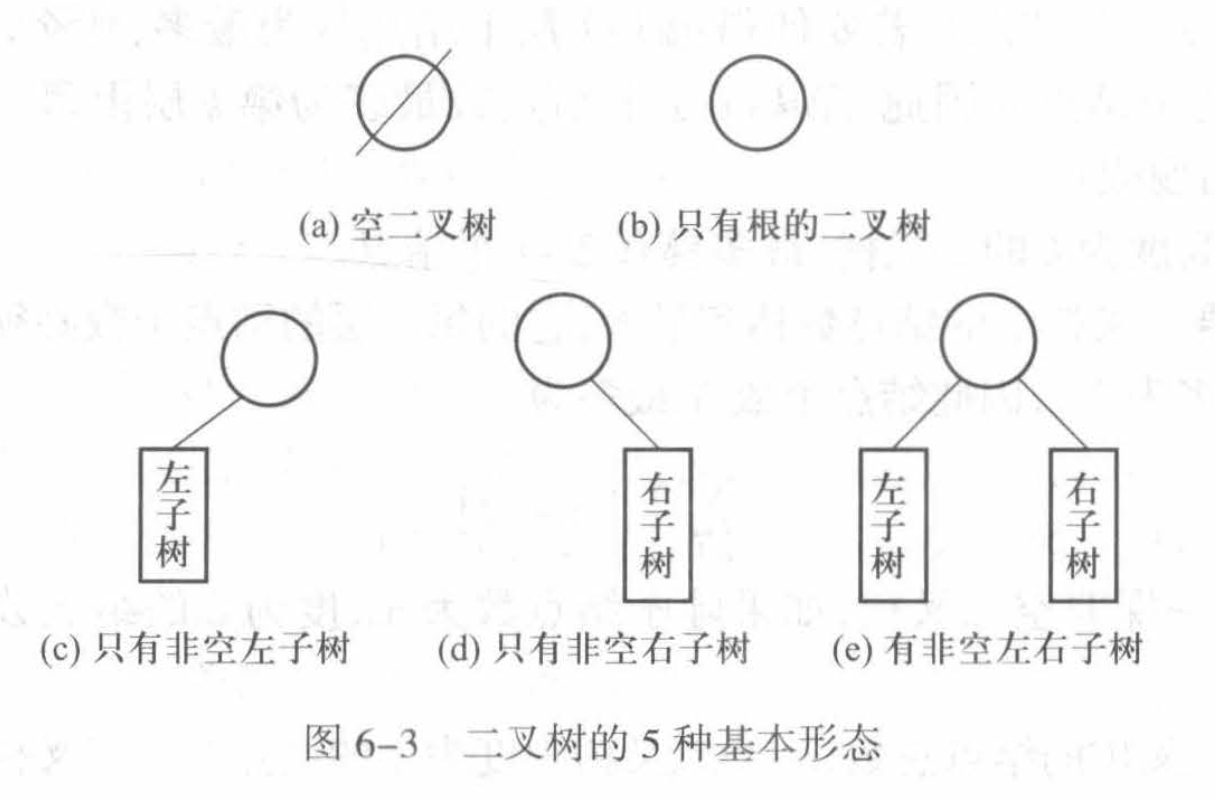
满二叉树:一棵二叉树中任意一层结点数量都达到了最大值
完全二叉树:在满二叉树的最底层自右向左依次去掉若干个结点(不能跳过任何一个结点)。即满二叉树一定是完全二叉树,但完全二叉树不一定是满二叉树。
下面是二叉树的一些常用性质:
1.一棵二叉树第i层最多有2^(i - 1)个结点
2.一棵高度为k的二叉树上,最多有2^k - 1 个结点
3.对于一棵非空二叉树,如果叶子结点数为n_0,度为2的结点数为n_2,则有n_0 = n_2 + 1
证明:设二叉树中度数为1的结点数量为n_1,结点总数为n,那么自然有:
n = n_0 + n_1 + n_2
再看树枝数量B,二叉树中每个结点(除根结点外)都有一根指向他们的树枝,所以有:
B = n - 1
这些树枝都是由度为1、2的结点发出的,所以
n_1 + 2 * n_2 = n - 1
所以
n_0 = n_2 + 1
4.具有n个结点的完全二叉树高度为[log_2 n] + 1
5.如果对一棵有n个结点的完全二叉树中的结点按层自上而下,每一层按自左至右依次编号,若设根结点的编号为1,则对任一编号为i的结点,有:
(1)若i = 1,则为根结点;若i>1,则父结点编号为[i/2]
(2)如果2i>n,则编号为i的结点为叶子结点,没有儿子;否则,其左儿子的编号为2i
(3)如果2i + 1>n,则编号为i的结点无右儿子;否则,其右儿子的编号为2i + 1
二叉树的基本操作
(1)create() 创建空二叉树
(2)clear() 清除二叉树中所有结点
(3)isEmpty() 判别空二叉树
(4)root() 找到二叉树根结点的值
(5)parent(x) 找到结点x的父结点值
(6)lchild(x) 找结点x的左结点值
(7)rchild(x) 找结点x的右结点值
(8)deLeft(x) 删除结点x的左子树
(9)deRight(x) 删除结点x的右子树
(10)traverse() 访问二叉树上每一个结点
对于最后一个操作——traverse(),我们有以下几种方式实现遍历:
- 前序遍历(先根遍历):先访问根结点,然后前序遍历左子树,然后前序遍历右子树
- 中序遍历(中根遍历):先中序遍历左子树,然后访问根结点,然后中序遍历右子树
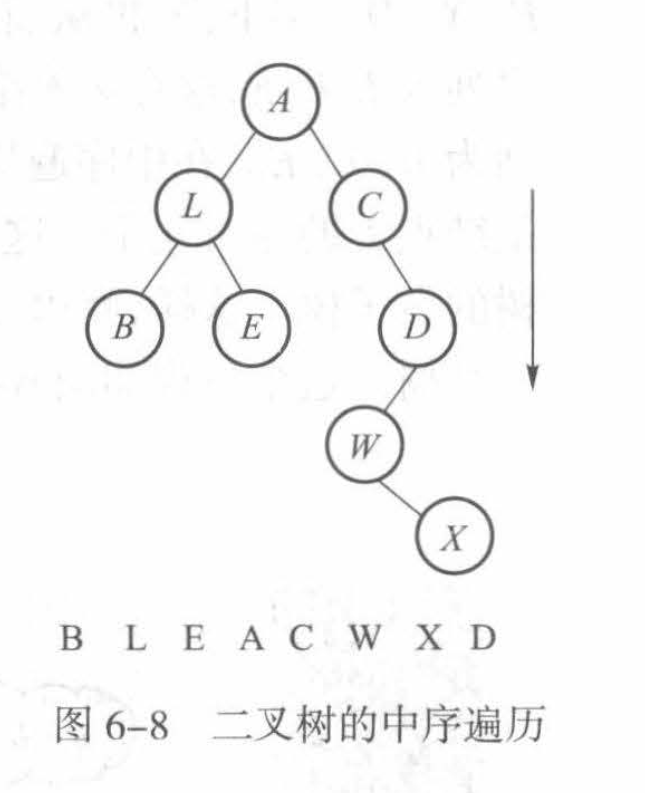
- 后序遍历(后根遍历):先后序遍历左子树,然后后序遍历右子树,最后访问根结点
- 层次遍历:在访问了第k层的所有结点后,再按从左到右的次序访问第k+1层
前序遍历+中序遍历可以确定一棵二叉树(通过前序遍历找到根结点,然后得到左子树右子树,下面就是递归了),同理,后序遍历+中序遍历也可以确定一棵二叉树,但前序遍历+后序遍历无法确定一棵二叉树(易举反例)
下面是二叉树的抽象类:
1 | |
二叉树的顺序实现
与线性结构一样,所谓的顺序存储就是将数据元素存放在一个数组中
若是完全二叉树,那显然用数组实现将会非常简单,结点的存储位置可以直接反应出结点的存储关系。
但如果需要存储的二叉树不是完全二叉树,情况就会比较不同。父子间数量关系(性质5)并不成立。可能的解决方案是在残缺位置上添加“虚结点”使之变成一棵完全二叉树。
如下图所示: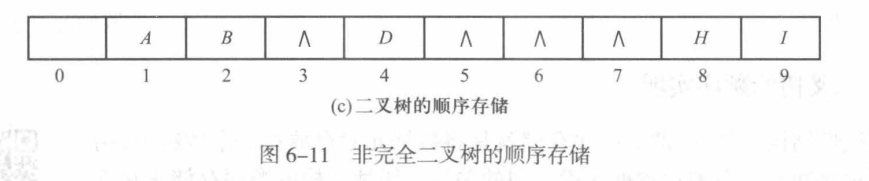
二叉树的链接实现
标准存储方式——二叉链表
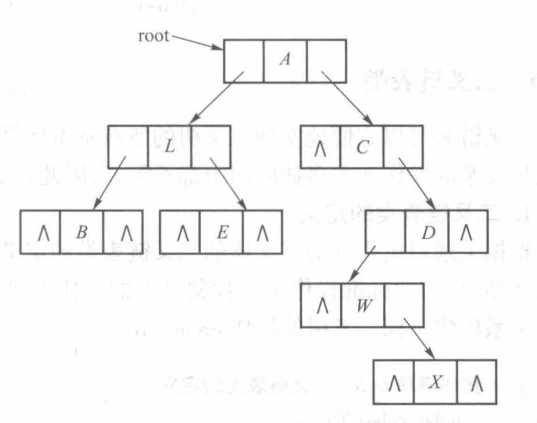
在二叉链表中,每个存储结点由3个字段组成,存储数据元素值的数据字段以及指向左、右儿子的指针字段。如下所示:
| left | data | right |
下面是二叉链表存储示例:
广义标准存储方式——三叉链表
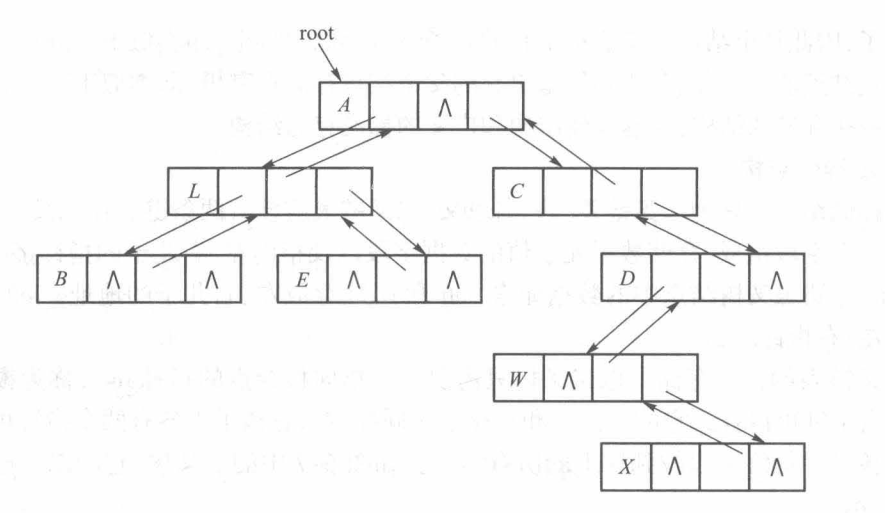
在标准存储结构的基础上,再增加一个指向其父亲结点的指针,这就是广义标准存储方式
| data | left | parent | right |
下面是三叉链表存储示例:
Conclude
由于二叉链表的简洁,且查找父亲的操作较为少见,所以我们更为常用的还是二叉链表