Data-Structure11

Before：全世界都在偶遇她，只有我没机会嘛😥

Data Structure 11 二叉链表遍历的非递归实现及二叉树的应用

二叉链表遍历的非递归实现

上一节翁阿姨的课上，我们讲到了通过栈对函数实现非递归调用，而今天所说的二叉链表遍历的非递归实现，同样也是依靠链接栈这一数据结构实现的。实现时需要注意进栈顺序的细节，下面给出代码实现。

template <class T>
void binaryTree<T>::preOrder() const{
    linkStack<Node *> s;
    s.push(root);
    while(!s.isEmpty()){
        Node *tmp = s.pop();
        cout << tmp -> data;

        if(tmp -> left != nullptr){
            s.push(tmp -> left);
        }
        if(tmp -> right != nullptr){
            s.push(tmp -> right);
        }
    }
}

而中序遍历在实现时则有一些不同，因为中序遍历要求先访问左子树，再访问根结点，最后访问右子树，所以在根结点出栈后不能先访问它，而将其暂存，先访问左子树，再访问它。为了解决这一问题，我们重新更换一种结点，记录结点进栈的次数。

struct StNode{
    Node *node;
    int timePop;
    StNode(Node *n = nullptr){
        node = n;
        timePop = 0;
    };
};

template <class T>
void binaryTree<T>::midOrder() const{
    linkStack<StNode> s;
    StNode current(root);

    while(!s.isEmpty()){
        current = s.pop();
        ++ current.timePop;
        if(current.timePop == 2){
            // 出栈2次了
            cout << current.node -> data << endl;
            if(current.node -> right != nullptr){
                current.push(StNode n(current.node -> right));
            }
        }else{
            // 重新被推回栈中
            s.push(current);
            if(current.node -> left != nullptr){
                current.push(StNode n(current.node -> left));
            }
        }
    }
}

最后是后序遍历，与中序遍历实现方法类似，但只有在第三次出栈时才会被访问

template <class T>
void binaryTree<T>::postOrder() const{
    linkStack<StNode> s;
    StNode current(root);

    while(!s.isEmpty()){
        current = s.pop();
        ++ current.timePop;

        if(current.timePop == 3){
            cout << current.node -> data << endl;
        }else if(current.timePop == 2){
            s.push(current);
            if(current.node -> right != nullptr){
                s.push(StNode n(current.node -> right));
            }
        }else if(current.timePop == 1){
            s.push(current);
            if(current.node -> left != nullptr){
                s.push(StNode n(current.node -> left));
            }
        }
    }
}

二叉树的应用——计算表达式

由于算术运算符是二元运算符，故可以很自然地表示成一棵二叉树，根结点表示运算符，左右孩子是运算数，这棵树被称为表达式树，既然如此，我们知道对这棵树的遍历是后序遍历
下面就是一棵表达式树：

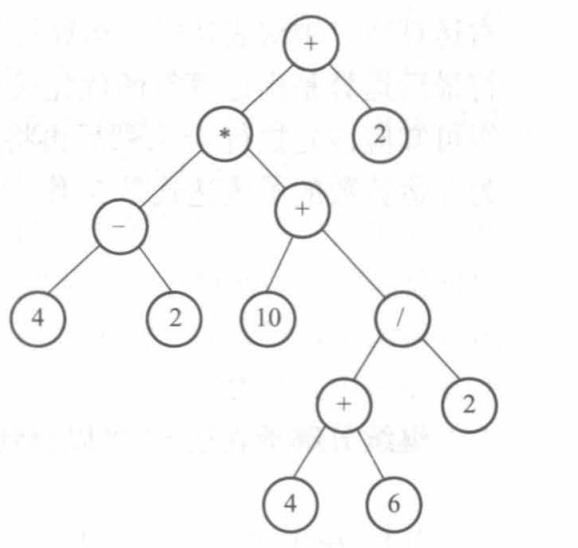
所描述的表达式为：**(4 - 2)(10 + (4 + 6)/2) + 2*

这个逻辑构造似乎还是比较好理解的，所以，我们就直接来看看如何建树吧。

class calc{
    enum Type{DATA,ADD,SUB,MULTI,DIV,OPAREN,CPAREN,EOL};

    struct node{
        Type type;
        int data;
        node *lchild,rchild;

        node(Type t,int d = 0,node *lc = nullptr,node *rc = nullptr){
            type = t;
            data = d;
            lchild = lc;
            rchild = rc;
        }
    };

    node *root;

    node *create(char *&s); //创建一棵表达式树
    Type getToken(char *&s,int &value); // 获得一个切片
    int result(node *t); //计算表达式结果

    public:
        calc(char *s){
            root = create(s);
        }

        int result(){
            if(root == nullptr){
                return 0;
            }
            return result(root);
        }
};

create函数的实现

calc::node *calc::create(char *&s){
    calc::node *p,*root = nullptr;
    Type returnType;
    int value;

    while(*s){
        returnType = calc::getToken(s,value);

        switch(returnType){
            case DATA:case OPAREN:
                if(returnType == DATA){
                    node *p = new node(DATA,value);
                }else{
                    p = create(s);
                }
                if(root != nullptr){
                    if(root -> rchild == nullptr){
                        root -> rchild = p;
                    }else{
                        root -> rchild -> rchild = p;
                    }
                }
                break;
            case ADD: case SUB:
                if(root == nullptr){
                    root = new node(returnType,0,p);
                }else{
                    root = new node(returnType,0,root);
                }
                break;
            case MULTI: case DIV:
                if(root == nullptr){
                    root = new node(returnType,0,p);
                }else if(root -> type == MULTI || root -> type == DIV){
                    root = new node(returnType,0,root);
                }else{
                    root -> rchild = new node(returnType,0,root -> rchild);
                }
                break;
            case CPAREN: caseEOL:
                return root;
        }
    }
    return root;
}

getToken 函数与先前在Bookstore-2024中写的TokenScanner类类似，故不描述了（好懒啊😅）

另一个比较有趣的函数——result

int calc::result(calc::node *t){
    int num1,num2;
    if(t -> type == DATA){
        return t -> data;
    }
    num1 = calc(t -> lchild);
    num2 = calc(t -> rchild);
    if(t -> type == ADD){
        t -> data = num1 + num2;
        return num1 + num2;
    }else if(t -> type == SUB){
        t -> data = num1 - num2;
        return num1 - num2;
    }else if(t -> type == MULTI){
        t -> data = num1 * num2;
        return num1 * num2;
    }else if(t -> type == DIV){
        t -> data = num1 / num2;
        return num1 / num2;
    }
}

Conclude

这两天一直在写二叉树，总结一下，真是对递归很巧妙的应用呢！
下面就是Huffman Tree了，离priority_queue越来越近了😝