Data-Structure12
Before:喜欢物理,喜欢数分,喜欢数据结构😋😋😋(疑似学了一天发疯)
喜欢日升日落,喜欢璀璨星河,喜欢得不到的你
Data Structure 12 哈夫曼树 树和森林
哈夫曼树和哈夫曼编码
背景:
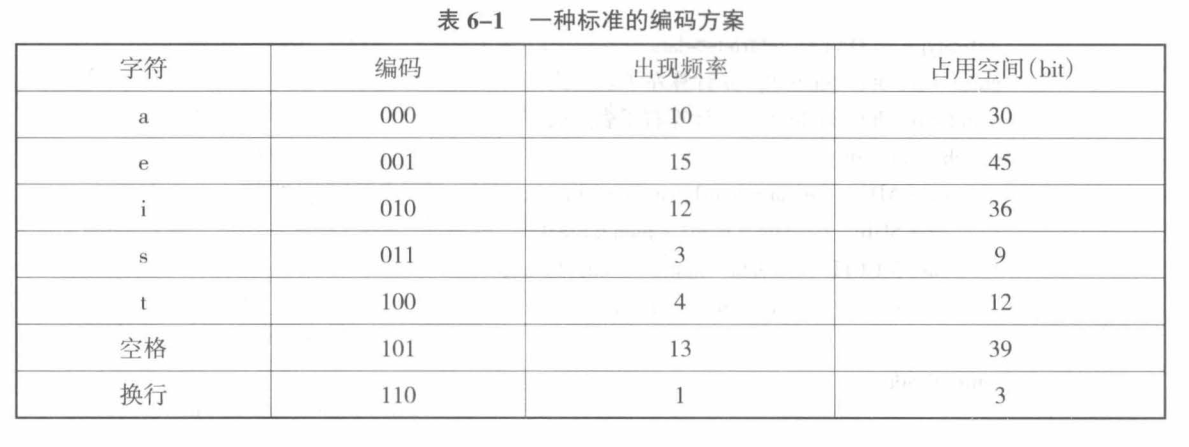
大多数计算机采用ASCII 编码,ASCII编码是一种等长的编码,每个字符的编码长度相同。但我们有一些常用的ASCII字符,也有一些较不常用的字符。如果所有字符均等长,将会造成保存文本空间较为庞大。所以我们可以让使用频率较高的字符拥有较短的编码,使用频率较低的字符拥有较长的编码,使得保存文本的空间减少。
举一个例子,现在有一个文本,下列字符的出现频率分别为:
a(10),e(15),i(12),s(3),t(4),空格(13),换行(1)
那么其占用的空间可以这样计算:
占用空间为:3*(10 + 15 + 12 + 3 + 4 + 13 + 1) = 174 bit
而若采用不等长编码,文本存储空间将会大大节省:
3 * 10 + 2 * 15 + 2 * 12 + 5 * 3 + 4 * 4 + 2 * 13 + 5 * 1 = 146 bit
那么如何找到这个优化的编码呢?可以先构建一棵哈夫曼树,再从哈夫曼树获得哈夫曼编码
哈夫曼树构建
我们构建一棵完全二叉树,在这棵树中,字符仅被存放在叶结点中,每个字符的编码是从根结点到叶结点的路径,0表示左子树,1表示右子树。
Example:如果从根结点出发,向右,向左,再向右,表示的即为101。
我们可以得到:若一个字符到根结点,经过的树枝数为L,在文本中出现的次数为w,则占用的存储空间为 L*w。每个字符总的存储量被定义为这个编码的代价。
按照上述建树的方式,我们可以将先前例子中的文本表示成一棵瓦努请安二叉树: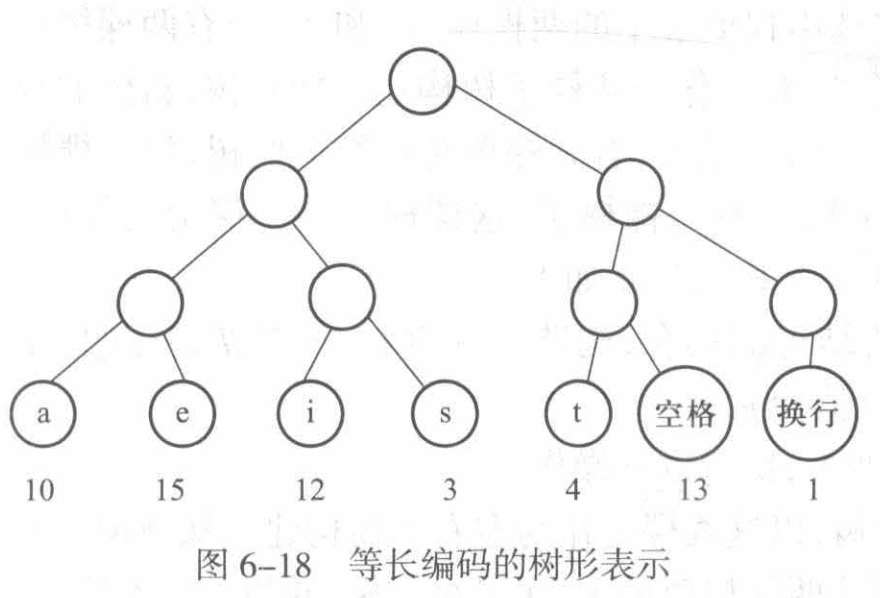
我们考虑对这棵树进行一些优化,比如可以看到换行字符的父结点只有一个子结点,故我们考虑将换行符移到其父结点的位置,这样换行符的存储空间就减小了 1bit,得到一个比原来更优的存储方案。这样一种存储方案其实还包含了字符间的一个性质:没有一个字符的编码会是另一个另一个字符编码的前缀。
换句话说,字符编码可以有不同的长度,只要每个字符的编码与其他任何字符编码的前缀不同即可。这种编码方式称为前缀编码。
上述问题的最优二叉树如下图所示:
我们要找到一棵最小代价的二叉树!!!
隆重推出:
哈夫曼算法
下面是Huffman Tree的构造规则:
假设有n个权值,则构造出的哈夫曼树有n个叶子结点。n个权值分别设为 w_1、w_2、… 、w_n。
(1)将w_1、w_2、… 、w_n看成是有n棵树的森林(每棵树仅有一个结点);
(2)在森林中选出根结点的权值最小的两棵树进行合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;
(3)从森林中删除选取的两棵树,并将新树加入森林;
(4)重复(2)、(3)步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树(最优二叉树)
哈夫曼树类的实现
我们采用动态数组来实现哈夫曼树,优势在于:父子节点关系可以通过下标计算,代码更简洁
思路已经很清楚了,就直接上代码了😋
1 | |
我们首先要实现哈夫曼树类中最重要的一个函数——构造函数,我们需要在构造函数中实现哈夫曼树的构建。
1 | |
getCode函数用来获得字符对应的Huffman编码
1 | |
搞定!是不是挺简单的😋
树和森林
不再是二叉树,而是n叉树,结点里该存什么?
树的存储实现
孩子链表示法
由于每个结点的孩子数量差异较大,如果开一个指针数组存孩子地址会造成大量空间的浪费,于是考虑用链表对所有子结点的地址进行存储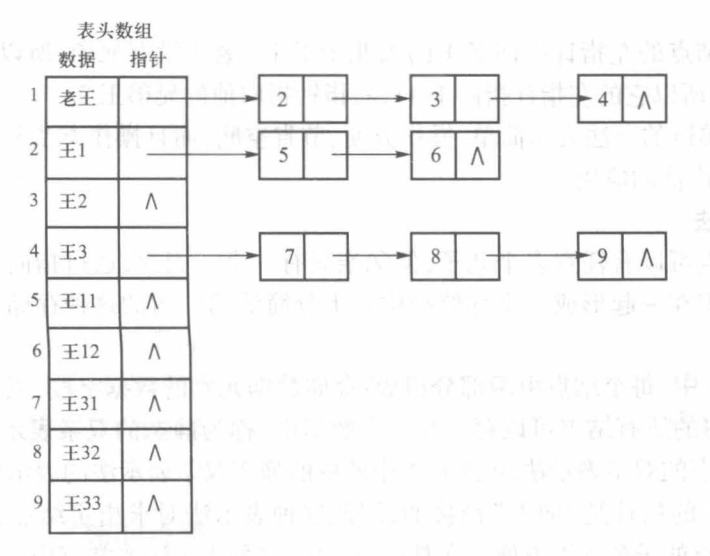
孩子兄弟链表示法(最常用的树的存储结构)
孩子兄弟链表示法中结点形式与二叉树一致,区别在于:左指针指向第一个儿子,右指针指向下一个兄弟(看到这里Jane不禁叫好,真是绝妙😝)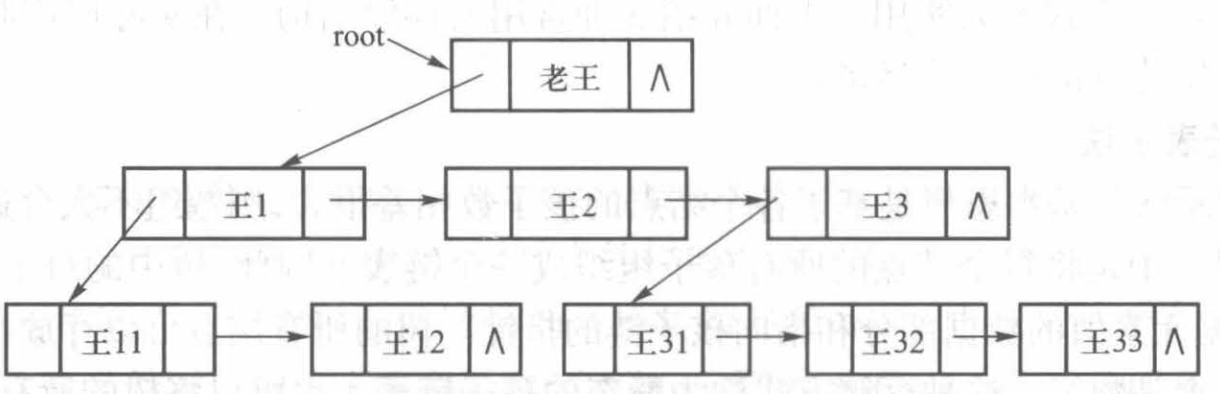
双亲表示法
树上每个结点可以有多个儿子,但只能有一个父亲。所以想法很简单,通过指向父结点的指针将整棵树组织起来。这个结构可以直接存在数组里。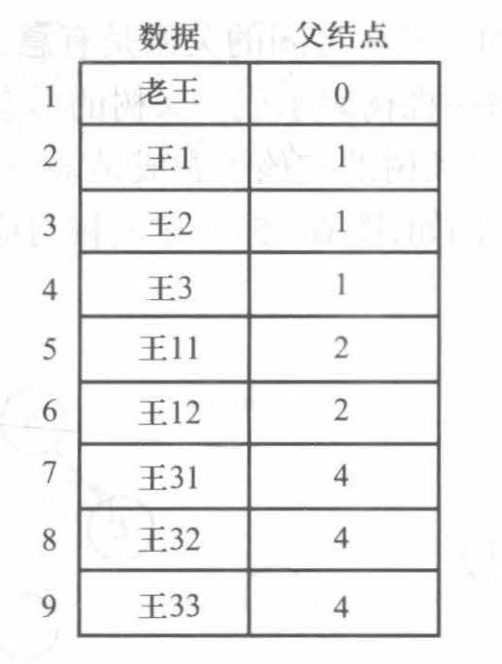
树的遍历
- 前序遍历
- 后序遍历
- 层次遍历
树、森林与二叉树的转换
树的孩子兄弟链表示法其实就可以把一棵树当成是二叉树进行考虑,把二叉树的左结点看作是第一个儿子,右节点看作是下一个兄弟。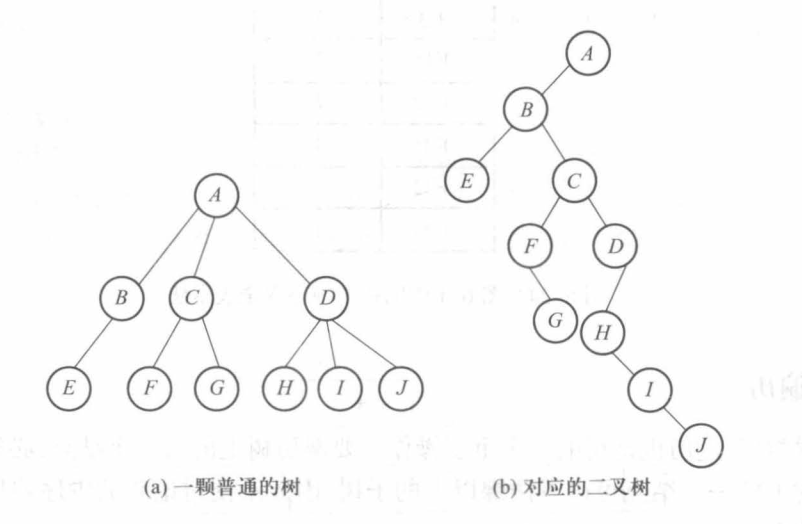
我们还可以将森林转化成一棵大二叉树,利用了一个性质:根结点没有兄弟,即根结点没有右子树,只需以下2步:
(1)将森林里每一棵树转化成二叉树
(2)将B_i 作为B_(i-1)根结点的右子树