Data-Structure13

Before：priority_queue终于启动了！

情书只有三行，爱意起于一瞬，结局愿是一生

Data Structure 13 优先级队列

优先级队列是什么？

元素之间的关系是由元素的优先级决定的，而不是由入队的先后次序决定。在优先级队列中，优先级最高的元素是队头元素，优先级最低的元素是队尾元素。

基于树的优先级队列

基于线性表的优先级队列入队出队的时间复杂度总有一个会到O(N)，我们不可以接受这个时间复杂度，所以：
我们介绍一种基于树状组织的优先级队列——二叉堆。它可以使入队和出队操作的最坏情况下时间复杂度是O(logN)。

优先级队列的存储实现

二叉堆

二叉堆是一棵满足结构性和有序性的二叉树，鉴于树状结构能给出指数的时间性能，所以将优先级队列组织成树是很自然的。我们需要保证树的高度尽可能小，所以这棵树最好是满二叉树，如果不满完全二叉树也可以。

完全二叉树可以采用顺序存储，利用父子结点的下标关系。另一个特性是有序性，堆的有序性是指最小的（或最大的）元素位于根的位置。

堆是一棵树，其每个节点都有一个键值，且每个节点的键值都大于等于/小于等于其父亲的键值。
当根结点是最小元素时，称为最小化堆，当根结点是最大元素时，称为最大化堆。在优先级队列中如果数值越小优先级越高，则采用最小化堆存储；反之，如果数值越大优先级越高，则采用最大化堆存储。

优先队列类的定义

template<class Type>
class priorityQueue: public queue<Type>{
    public:
        priorityQueue(int capacity = 100);
        priorityQueue(const Type data[],int size);
        ~priorityQueue();
        bool isEmpty() const;
        void enQueue(const Type &x);
        Type deQueue();
        Type getHead() const;
    
    private:
        int currentSize; //队列中元素个数
        Type *array; //二叉堆数组起始地址
        int maxSize; //数组规模
    
    void doubleSpace();
    void buildHeap();
    void percolateDown(int hole);
};

优先队列的运算实现——以大根堆为例

首先是不带初始数据构造函数、析构函数、判空和取首函数

template<class Type>
priorityQueue<Type>::priorityQueue(int capacity = 100){
    array = new Type[capacity];
    maxSize = capacity;
    currentSize = 0;
}

template<class Type>
priorityQueue<Type>::~priorityQueue(){
    delete []array;
}

template<class Type>
bool priorityQueue<Type>::isEmpty() const{
    return currentSize == 0;
}

template<class Type>
Type priorityQueue<Type>::getHead(){
    if(!isEmpty()){
        return array[1];
    }else{
        return -1;
    }
}

enQueue操作，即入队的过程，我们把它称作向上过滤，这种实现方法是在下一个可用的位置创建一个空结点，然后把它沿着堆往上冒，这个过程的时间复杂度是O(logN)。

template<class Type>
void priorityQueue<Type>::enQueue(const Type &x){
    if(currentSize == maxSize - 1){
        doubleSpace();
    }
    int pos = ++currentSize;
    while(pos != 1){
        if(array[pos] > array[pos/2]){
            int tmp = array[pos];
            array[pos] = array[pos/2];
            array[pos/2] = tmp;
            pos /= 2;
        }else{
            break;
        }
    }
}

deQueue操作，即出队的过程，二叉堆中我们要做的是删除根结点。我们的核心思想是：把根结点和完全二叉树中的最后一个结点交换值，然后删除最后一个结点，将根结点分别与左右结点进行比较，把它沿着堆往下过滤，这一过程称为向下过滤，时间复杂度同样是O(logN)。

实现这一过程，我们需要调用一个私有成员函数void percolateDown(int hole);

template<class Type>
Type priorityQueue<Type>::deQueue(){
    //交换
    Type deNode;
    deNode = array[1];
    array[1] = array[currentSize - 1];
    percolateDown(1); //向下过滤根结点

    return deNode;
}

template<class Type>
void priorityQueue<Type>::percolateDown(int hole){
    while(2 * hole <= currentSize){
        if(hole * 2 + 1 <= currentSize){
            //说明左右结点均存在
            Type tmp;
            int x;
            if(array[2 * hole + 1] < array[2 * hole]){
                tmp = array[2 * hole];
                x = 2 * hole;
            }else{
                tmp = array[2 * hole + 1];
                x = 2 * hole + 1;
            }
            if(tmp > array[hole]){
                Type t = array[hole];
                array[hole] = tmp;
                array[x] = t;
                hole = x;
            }else{
                break;
            }
        }else{
            //只有左结点存在
            if(array[hole] > array[2 * hole]){
                Type tmp = array[hole];
                array[hole] = array[2 * hole];
                array[2 * hole] = tmp;
                hole = 2 * hole;
            }else{
                break;
            }
        }
    }
}

最后就是如何构造这个二叉堆了
最简单的做法是执行N次enQueue操作（类似于二分查找），时间复杂度达到了O(NlogN)，考虑一种复杂度更低的建堆方法。

我们可以从编号最大的非叶结点开始，对结点进行向下过滤，这样计算下来的时间复杂度来到了O(N)（具体推导可见Introduction to Algorithms）

template<class Type>
void priorityQueue<Type>::buildHeap(){
    for(int i = currentSize / 2;i >= 1;i--){
        percolateDown(i);
    }
}

template<class Type>
priorityQueue<Type>::priorityQueue(const Type data[],int size){
    currentSize = size;
    maxSize = size + 10;
    array = new Type[maxSize];
    for(int i = 1;i <= currentSize;i++){
        array[i] = data[i - 1];
    }
    buildHeap();
}

However

我觉得这样写却有一些不美观，虽然利用数组下标节省了很多空间，但在处理归并堆时，使用数组就不太合适了，所以priority_queue同样可以用二叉链表实现，而且我们可以将push和pop的操作都统一到merge里去，就非常简洁了。

我在STLite2025——priority_queue类的实现中用了一个二叉链表来实现大根堆（实则维护了一棵左偏树）。害还不是因为一定要归并队列，不然谁还用链表写啊（真占内存）

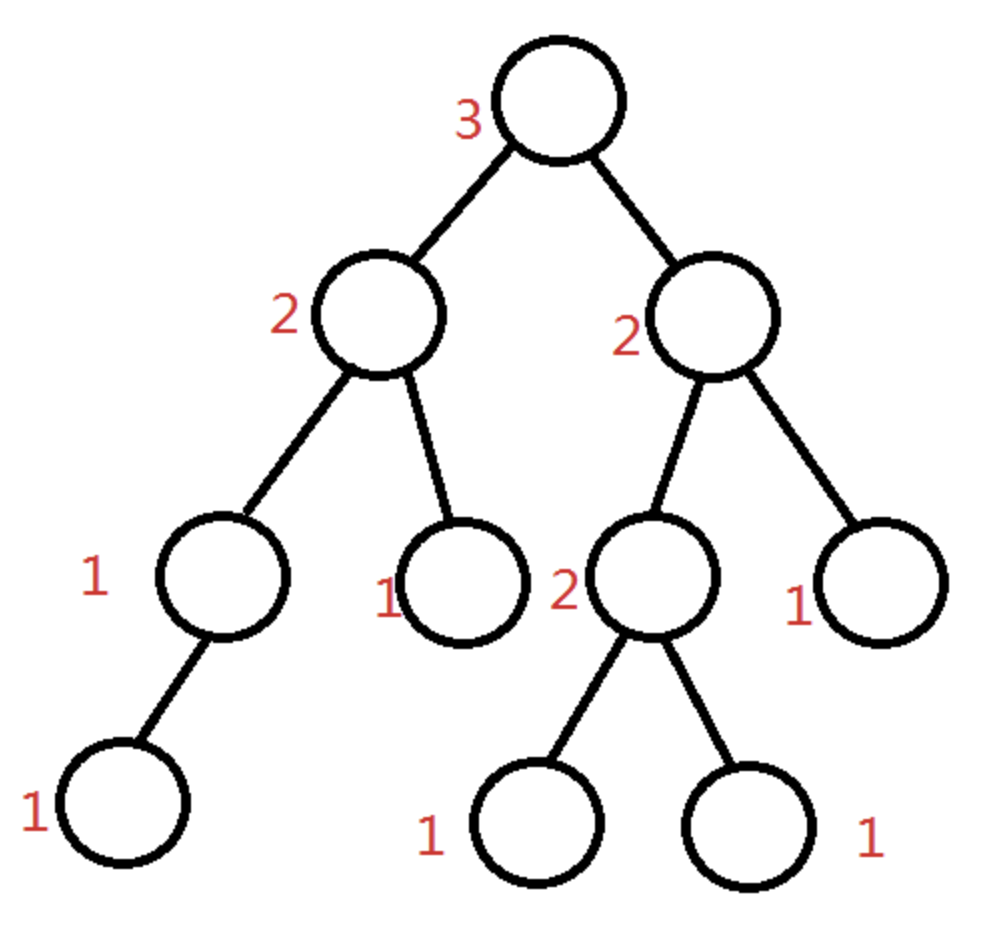
先介绍一下左偏树（也可以叫左偏堆）
左偏树具有堆的性质，优点在于可以快速合并。对于一棵二叉树，我们定义外节点为子节点数小于两个的节点（省流：有空子节点的结点），定义一个节点的 dist 为其到子树中最近的外节点所经过的边的数量。空节点的 dist 为0。
特别注意：左偏树并不是一棵完全二叉树，故dist与树的深度没有关系

如下图所示，这是一棵左偏树：

这，也是一棵左偏树：

左偏树作为一个可并堆，核心操作在于归并堆merge操作：

Node *mergeHeap(Node *l,Node *r) {
    if(l == nullptr) {
        return r;
    }
    if(r == nullptr) {
        return l;
    }
    if(Compare()(l -> data,r -> data)) {
        std::swap(l ,r ); //这一步是为了维护左子树的根结点一定较大
    }

    l -> right = mergeHeap(l -> right,r);
    // 这一步将左子树的右子树与右子树合并，这样左偏值最多增大 1
    if(l -> left == nullptr) {
        std::swap(l -> left, l -> right);
    }else if(l -> right != nullptr && l -> left -> dist < l -> right -> dist) {
        std::swap(l -> left, l -> right);
    }

    if(l -> right == nullptr) {
        l -> dist = 0;
    }else {
        l -> dist = l -> right -> dist + 1;
    }
    return l;
}

merge操作合并两个大小分别为 n 和 m 的堆复杂度是O(logN + logM)，实现了对数级复杂度

其他可并堆

斜堆

斜堆是满足堆的有序性，但没有任何平衡条件限定的二叉树。在斜堆中，不能保证树的深度是对数的。但从平均的概念上能够保证所有的操作都是对数的时间性能。它比左偏堆简单，不需要为结点保存空路径信息。

归并策略是：根结点值比较大的堆与根结点比较小的堆的右子堆归并，在完成一个归并前，对产生的临时树的右路径上的每个结点交换它们的左右孩子。

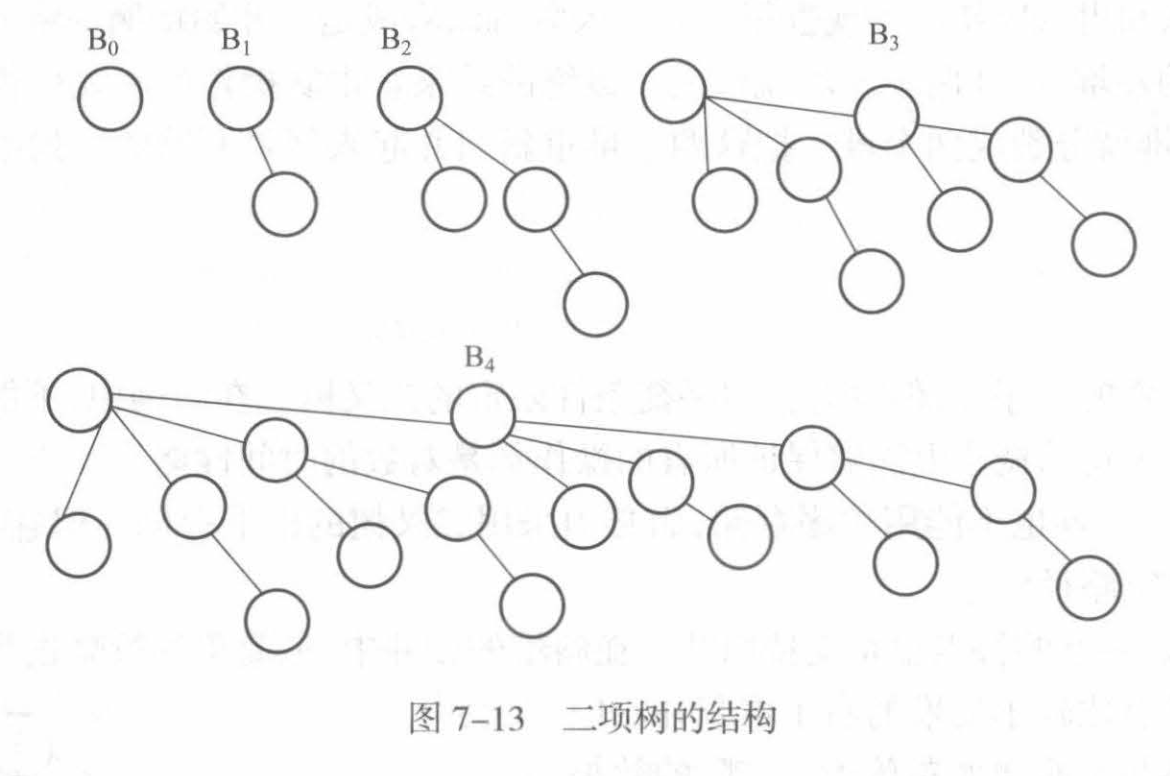
二项堆

二项堆不是用一棵满足堆的有序性的二叉树表示，而是用一个森林表示。森林中的每一棵树都有一定的约束，称为二项树。二项树是满足堆的有序性的树。高度为0的二项树是只有根结点的树，高度为k的二项树凡是将一棵B_(k - 1)加到另一棵B_(k - 1)的根上形成的。在这片森林中，每个高度的二项树之多只有一棵。

从二项树的特性可以看出，对给定的元素个数，可以构造唯一的一个二项堆。（二进制表示整数）
二项堆的归并操作：由低到高依次归并两个优先级队列中高度相同的树，也就是归并两个二项堆中对应的树。入队操作可以看成是归并的特例，出队操作只需删除最小根结点的二项树，将其裂成一个二项堆，再将其与原有二叉堆合并即可。

END

树状结构正式结束！明天（尽量）进入集合结构！

Reference

https://oi-wiki.org/ds/heap/
https://oi-wiki.org/ds/leftist-tree/
https://www.luogu.com.cn/article/uoeyv3gq