Mathematical-Logic2
Before:哎呀数理逻辑真的好抽象😭本来英语就烂,还有一大堆新定义的符号,绕在一起,感觉更像是在学语言而不是数学😥再加上周五晚上连上3节😅
Result:果断重开了
Decision:我一定要用中文把这门课搞清楚,抵制洋文!!!
Mathematical Logic 2 一阶逻辑的语义
Structure 结构
在不同的场合下,同一个一阶逻辑命题可能有不同的含义。如对∀v0Rv0v0,既可以解读成“任意自然数都整除自己”(真),也可以解读成“任何实数都小于自己”(假)
So:讨论语义时首先需要确定讨论的数学对象
刚刚的例子中,自然数和实数明确了讨论对象取自怎样的集合,这个集合称作域(universe),记为A
确定符号集中每个符号的含义,就是确定每个符号对应的元素、集合或映射具体是什么:
- 一个n元关系就是某个A^n的子集 a(R)
- 一个n元函数就是某个A^n到A的映射 a(f)
- 每个常数符号对应A中某个特定元素 a(c)
我们把这个从符号到其具体含义的映射记为a。
A 和 a 确定了一阶逻辑中变量的“定义域”和符号集中每个符号的含义。我们把二元组(A,a)记为 𝔄,称作S-结构。
对于符号集S = {R,f,c},我们通常将a(R)写作$R^𝔄$或$R^A$,a(f)写作$f^𝔄$或$f^A$,a(c)写作$c^𝔄$或$c^A$。
Interpretation 解释
Structure给出了变量的定义域和符号集的语义,但我们接下来还有terms和formulas
一个term的语义是从一个term到universe中一个元素的映射——$\beta$
为了确定这个映射,我们首先需要知道term中的每个变量代表universe当中的哪个元素,这就是要我们给出一个$v_i$ -> A 的映射$\beta$
所以我们把一个S-structure和一个S-assignment的二元组称作I = (𝔄,$\beta$)
定义解释的语义
- 对于变量x,I(x) = $\beta$(x)
- 对于常量c,I(c) = $c^𝔄$
- 对于n元函数关系f $\in$ S,$t_1,t_2,…,t_n$均为S-terms。那么有I(ft_1 … t_n) = $f^𝔄$(I(t_1),I(t_2),…,I(t_n))
formula的语义是从一个term到“真或假”的映射(类似于bool?)
对于一个formula 𝜑 ,我们用记号 I |= 𝜑 来表示 公式 𝜑 的语义为真,读作I 满足𝜑 ,|= 即称为满足关系。( 解释 I 满足公式 𝜑 )
下面是一些原子性/关于逻辑连词/量词的情况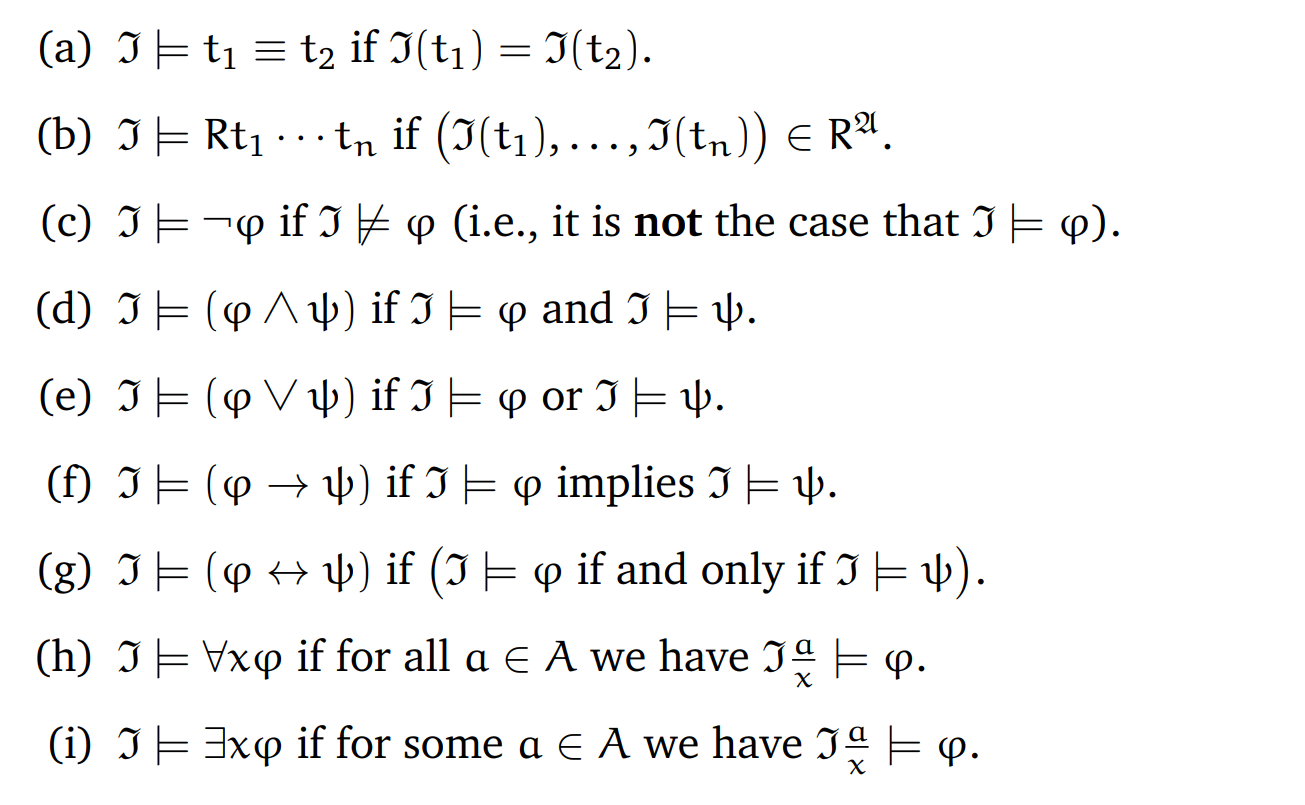
(a) 当且仅当I(t_1),I(t_2)是universe下的同一个元素
(b) 当且仅当 (I(t_1),…,I(t_n)) 属于$R^𝔄$
(c) 当且仅当 解释I 不满足公式 𝜑
(d) 当且仅当 解释I 满足公式 𝜑 且 解释I 满足公式Ψ
(e) 当且仅当 解释I 满足公式 𝜑 或 解释I 满足公式Ψ
(f) (一个有点神奇的解释)当且仅当 I |= φ(语法上)表明解释I 满足公式 𝜑 (语义上)
(g) 当且仅当(还有一个当且仅当,亿点点绕)(解释I 满足 公式 𝜑 当且仅当解释I 满足公式Ψ)
比较复杂的就是 ∀ 和 ∃
(h) 想说的意思是:当且仅当universe中每个元素为公式 𝜑 中出现的x赋值并保持其他变量赋值不变,公式 𝜑 始终不变
为此我们定义一个描述为formula中的某个特定变量赋特殊的值的方便的符号: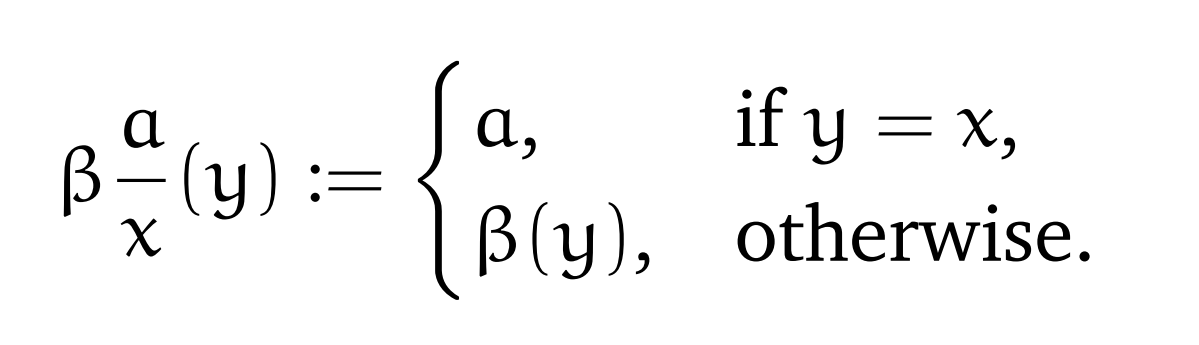
于是新的解释I 变为了: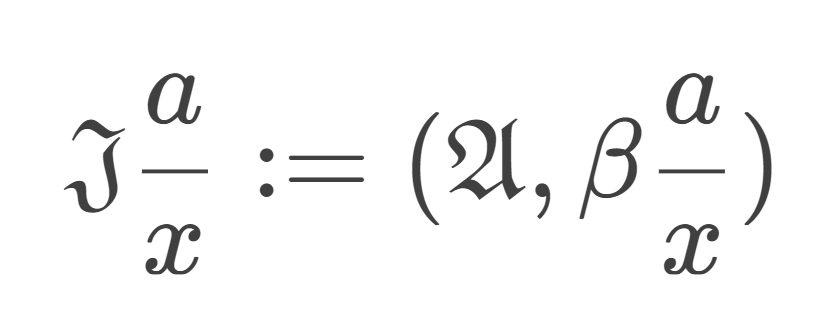
这表示在解释I 中,将变量 𝑥 的赋值修改为 𝑎,其他部分保持不变。
于是(h)表示的即为:对于域 𝐴中的每一个元素 𝑎,如果将 𝑥 赋值为 𝑎,公式 𝜑 都为真。
(i) (也是同理)存在域 𝐴中的一个元素 𝑎,如果将 𝑥 赋值为 𝑎,公式 𝜑 为真。
如果一个公式 𝜑 是valid(恒真),那么所有的解释都能满足公式 𝜑
逻辑推论的定义:
Φ 是一个S-公式的集合;
公式 𝜑 是一个单独的S-公式
如果 Φ |= 𝜑,表示 𝜑 是 Φ 的逻辑推论,即公式 𝜑 可以从 Φ 中逻辑推导出来
我们称公式 𝜑 是可满足的,如果存在一个S-解释I,使得公式 𝜑 在解释I下为真
公式 𝜑 和公式 Ψ 是逻辑等价的,如果 𝜑 |= Ψ 且 Ψ |= 𝜑
Reference
这位博主真的救命,讲的太清楚了