Introduction to Algorithms1

Before：去年12月从班主任口中得知了我们的主角——MIT 6.006 Introduction to Algorithms这门非常经典的课（被誉为“MIT-EECS系的瑰宝”）。室友 @three-hats-user 同学在我的推荐下（自己没学别人学了🤡）在寒假卷了这门课（虽然还没学完），对它评价也很高。于是今天入手了这门课，一句话：不愧是MIT EECS🧎‍♀️🧎‍♀️🧎‍♀️另外，鉴于这门课程全部学完需要100hr，且有些算法在上学期的上机课中已经有所接触，故JaneZ并不会更新全部（有空一定会学完的呜呜呜），而是挑选一些结合这学期所学的数据结构的课程，提升辣鸡的算法能力😭😭😭

Introduction to Algorithms 1 Heaps and heap sort

Priority Queues Definition

A data structure implementing a set S of elements,each associated with a key,supporting the following operations:

• insert(S,x)
• max(S)
• extract_max(S):return element of S with largest key and remove it from S
• increase_key(S,x,k):increase the value of element x’ s key to new value k

Priority Queues can be built by using Heap or AVL.

Heap

As I said seconds before,Heap is one of the Implementations of a priority queue.

First,we are going to visualize an Array as a nearly complete binary tree（完全二叉树）

Let’s just talk about Max Heap here（Min Heap is exactly the same）

Max Heap Property:The key of a node is $\geq$ than the key children.
For example:

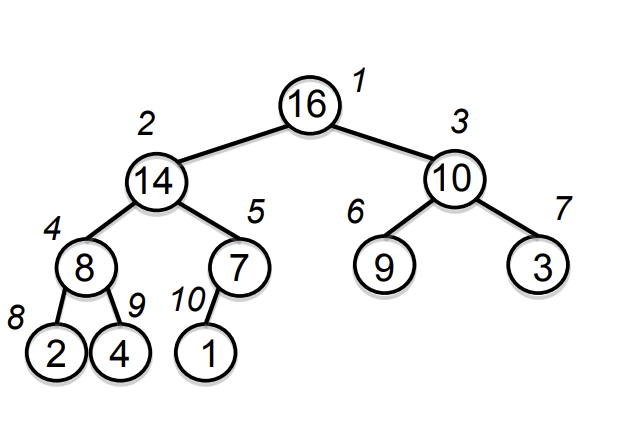
Almost the same basic characteristics as Binary Tree

Here’re some simple Heap Operations:

• build max heap: produce a max-heap from an unordered array
• max_heapify: correct a single violation(违反) of the heap property in a subtree at its root
• insert,extract_max,heapsort

The most important procedure: Max_heapify

• Assume that the trees rooted at left(i) and right(i) are max-heaps.

• If element A[i] violates the max-heap property, correct violation by “trickling” element A[i] down the tree, making the subtree rooted at index i a max-heap.

Here is an example of Max_heapify: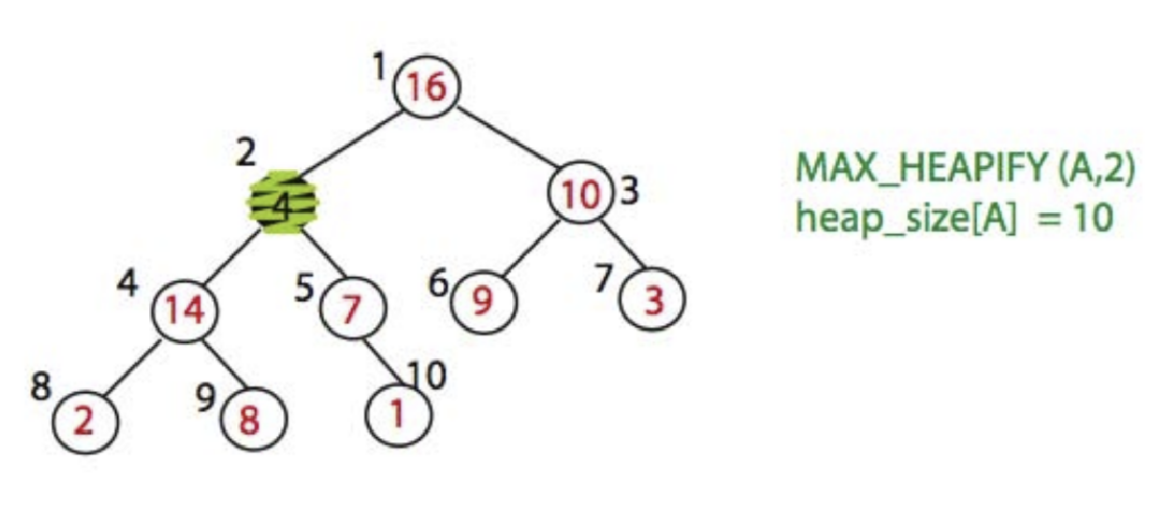

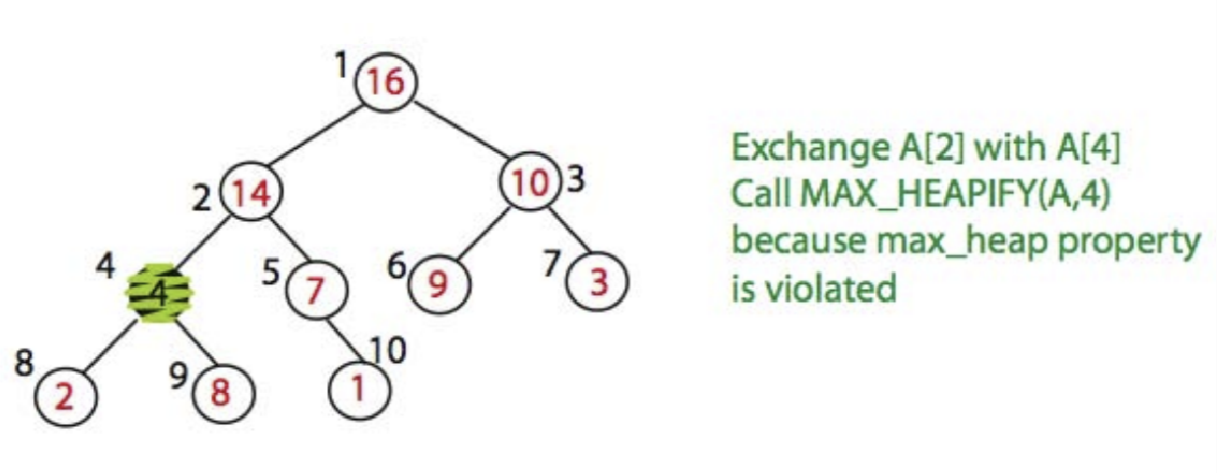
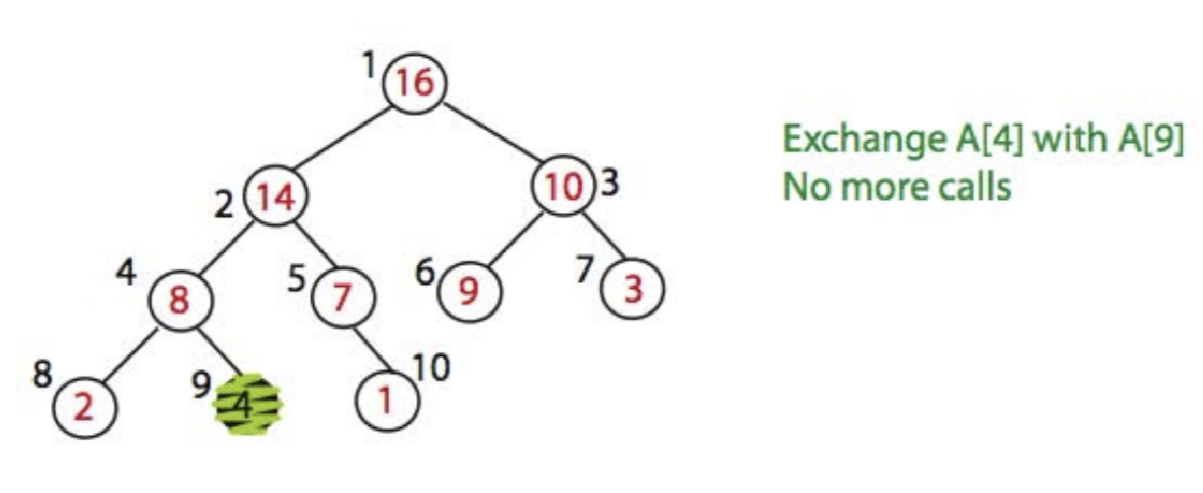
Time Complexity: O(logN)

Build Max Heap

For n/2 to 1 //从后往前第一个非叶节点开始
do Max_heapify(A,i)

这里我们很容易“看出”时间复杂度是O(NlogN)，然而真的如此嘛？
可以想一下，最底一层的非叶结点进行的操作次数至多只有1次，而并非logN次，只有根结点才会进行logN次操作，所以经过数学推导，我们可以验证，建堆操作的时间复杂度是O(N)

Heap Sort

I think it’s just a simple use of Max_Heap.Easy to understand and I will just show the thoughts.
(1)Build Max_Heap from an unordered array.
(2)Find A[1] (the biggest element)
(3)Swap elements A[1] and A[n]
(4)Discard(移除) n from the heap
(5)Run MaxHeapify to fix the missing 1 place
(6)Go to Step 2 until empty

The time complexity of Heap Sort is O(NlogN)

Last

这节的内容整体还是挺容易的，特别是在写完priority_queue之后😋
Keep Going!