Data-Structure14

Before：Long Time No See!这周前几天一直在小作业、数分作业、物理作业、物理实验（依托），到了周四也算是闲下来了，有了一大把自学的时间😋😋😋这周还是挺不错的？珍惜能天天见面的日子吧🥰Waiting always comes to an end.你是我声色张扬下欲盖弥彰的温柔理想。

Data Structure 14 集合与静态查找表

集合的定义

首先，集合中数据元素的关系十分松散，除了属于同一集合外，没有任何逻辑关系。但集合中的元素有一个区别其他元素的唯一标识，通常称为键值或关键字值。故每个集合中的元素可以看成由两部分组成：关键字值和其他信息。
故我们可以这样定义集合中元素的类型：

template<class KEY,class OTHER>
struct SET{
    KEY key;
    OTHER other;
};

由于集合中元素不存在直接前驱、直接后继等，故集合中的主要操作只有添加元素、删除元素以及查找某个元素是否出现在集合中。但当集合元素非常多时，查找某个元素将花费很长时间，我们需要一种手段来加速查找过程。因此将集合中的元素按它的唯一标识排序也是集合的基本运算。

查找的基本概念

通常将用于查找的数据结构称为查找表。查找就是要确定指定关键字值的数据元素在查找表中是否存在。（注意，有一些特殊的情况可能会出现一些数据结构含有相同关键字值，这样的集合称为多重集，我们暂不讨论这种情况）。
如果查找表中的数据元素个数和每个数据元素的值是不变的，这样的查找表我们通常称为静态查找表。如果对查找表不但要进行查找操作，还要进行插入、删除操作，那么查找表将是动态变化的，其数据元素的个数并不是一个稳定的常数，这样的查找表通常称为动态查找表。
显而易见，动态查找表的要求更高呢😢不仅要查找迅速，插入删除也要迅速（已经开始😇）

被查找的所有数据元素全部存放在内存储器中时的查找操作称为内部查找，如果数据元素太多，不能全部放在内存之中，只能将它们存放到外存储器中去，这时的查找操作便称之为外部查找。在外存储器中，每个数据元素通常称为记录。
在内部查找中，一般以比较次数作为衡量时间性能的一个标准。在外部查找中，被查找的数据是存储在外存储器上，查找时必须把外存储器上的数据读入内存。与外存访间相比，比较时间是微不足道的，所以在外部查找中一般以外存储器的访问次数作为衡量标准。减少访问外存的次数，将会大大减少查找的时间代价。

如果没记错（就是没记错），BPT也是要在外存上实现的吧。。。😇😇😇😇😇

静态查找表

数据元素个数及数据元素的值不允许变化的查找表称为静态查找表。（嗯几秒前刚讲过🤣）通常将被查找的数据存放在一个数组或顺序表中。

与其他各类数据结构一样，各个静态查找表中的数据元素类型是不一样的，因此，查找函数应该是一个函数模板。模板参数是数据元素的类型。静态查找表可以存放在一个数组中，也可以存放在 C+＋的标准模板库中的类模板vector中。

无序表的查找——顺序查找

由于无序表中元素无序，只能顺序查找按顺序检查保存在数组中的集合元素，直到找到一个匹配为止。

template<class KEY,class OTHER>
int seqSearch(SET<KEY,OTHER>data[],int size,const KEY &x){
    data[0].key = x;
    for(int i = size;data[i].key != x;i --);
    return i;
}

注意：这样写少了一次检查下标是否合法的比较，利用0处作为哨岗
时间复杂度为O(N)

有序表的查找

当集合中的元素是按照关键字值的次序存放在数组时，称为有序表。

顺序查找

以按递增顺序存储为例

template<class KEY,class OTHER>
int seqSearch(SET<KEY,OTHER>data[],int size,const KEY &x){
    data[0].key = x;
    for(int i = size;data[i].key > x;i --);
    if(data[i].key == x && i != 0){
        return i;
    }
    return 0;
}

二分查找

template<class KEY,class OTHER>
int seqSearch(SET<KEY,OTHER>data[],int size,const KEY &x){
    int low = 1;
    int high = size;
    int mid;
    while(low <= high){
        mid = (low + high)/2;
        if(data[mid] == x){
            return mid;
        }else if(data[mid] < x){
            low = mid + 1;
        }else{
            high = mid - 1;
        }
    }
    return 0;
}

时间复杂度为O(logN)

插值查找

假设分布均匀，则可利用公式判断位置：
next = low + (high - low + 1)*(x - a[low])/(a[high] - a[low])
但缺点同样很明显：计算太繁杂了（鼠鼠现在的算力手算兴许是算不出来的吧🤣🤣🤣）
所以使用插值查找需满足2个假设：
1.访问一个数据元素必须比一个典型的指令费时得多。例如，数组可能在磁盘里而不是在内存里，而且每次比较都需要访问一次磁盘。
2.这些数据必须不仅有序，而且分布相当均匀，这可以使每次估计都相当准确。

分块查找😋😋😋

这不是小作业刚做完的嘛嘻嘻，爽到了🥰🥰🥰
这不是Bookstore的文件存储测试，可爱的（逆天的阴间的）BlockList嘛🤣现在还挺喜欢BlockList的，笑死了，感觉还是挺好写的嘻嘻嘻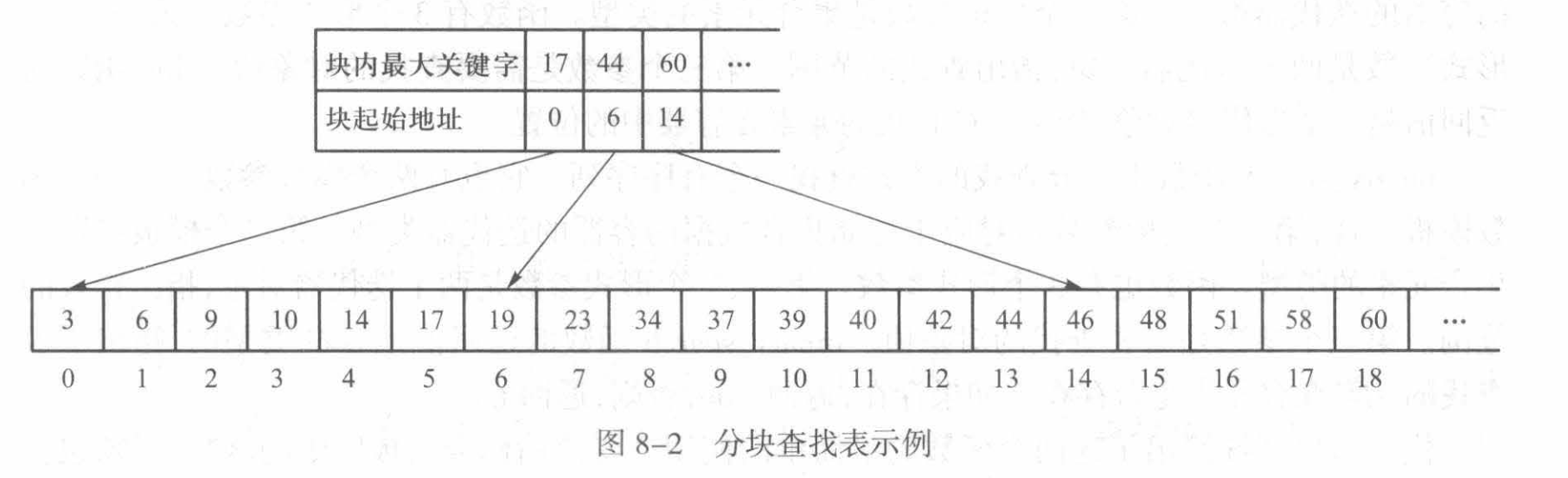

这张图真是太清楚了，如果早点看到，一切就会不同吧😥
总结一下，分块查找分两个阶段。先查找索引表，确定数据所在的块。由千索引表是有序的，可以采取顺序查找或二分查找。第二步是块内查找。如果块内是有序的，可以采用二分查找。如果块内是无序的，则只能采用顺序查找。
挺简单的，这是真心话，真简单，真的太简单了。真服了🤡

时间复杂度即便都采用顺序查找，也可以达到O(sqrt(N))，还是很快的？
尽情期待B PLUS TREE~~~

STL不给用，就不说了（也没啥值得说的bushi）