Introduction-to-Algorithms3
Before: 哎帮人debug好累啊,边改别人的代码边学AVL,也是无敌了。我到底要不要见她一面呢?感觉错过了就是一辈子😢😢😢
Introduction to Algorithms 3 Balanced Binary Search Tree——AVL
First, recall an important definition of Height of a Node: length of the longest downward path to a leaf
The Importance of Being Balanced
As we talk about last time,BST suppports insert/delete/min/max/next_larger/next_smaller or in a time complexity of O(h).But that’s not what we want.Somehow if h equals to n,it’s gonna be really bad.
We love this tree😋😋😋:
We hope to do some adjustments to the tree so that h can equal to logN.
AVL Trees——Adel’son-Vel’skii & Landis 1962
Main Defintion:
For every node,require heights of left & right children to differ by at most ± 1.
- We mark nil trees as height -1(quite smart cuz -1 + 1 = 0)
- Each nodes stores its height
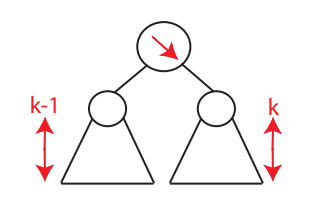
Balance
Consider the largest height of an AVL tree with N nodes.(worst time complexity)
Equalently,we can consider the minimun node numbers of an AVL tree with height h!
Great thoughts!
We can do a rough Maths proof:
N_h = N_(h - 1) + N_(h - 2) > 2N_(h - 2)
=> N_h > 2^(h/2)
=> h < 2 log(N_h)
So proved that h is alogN(a is a parameter)
Theoretical computer scientists can do this more accurately,like what the picture below shows using Fibonacci:
AVL insert
1.insert as in simple BST(just the normal one)
2.work your way up tree, restoring AVL property(the most important step of building the AVL tree)
Each Step of the famous AVL Rotation:
suppose x is lowest node violating(违背) AVL
assume x is right-heavy (left case symmetric)
if x’s right child is right-heavy or balanced:

else: follow steps
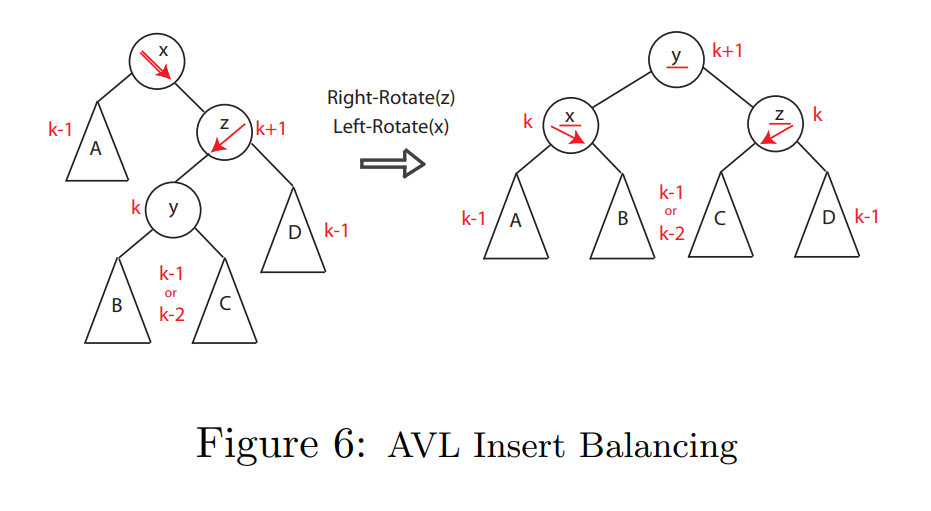
then continue up to x’s grandparent, greatgrandparent
Other Balanced Trees
- B-Trees/2-3-4 Trees Bayer and McCreight 1972 (see CLRS 18)
- BB[α] Trees Nievergelt and Reingold 1973
- Red-black Trees CLRS Chapter 13
- Splay-Trees Sleator and Tarjan 1985
- Skip Lists Pugh 1989
- Scapegoat Trees Galperin and Rivest 1993
- Treaps Seidel and Aragon 1996
Comparison with Heap

