Data-Structure15

Before: Am I noisy?I really regret.Why am I being so annoying?Why am I becoming jealous of something unnecessary?Maybe it’s because of something romantic,something secret,something I keep chasing,and that is you.Sometimes I find out that she is not that perfect,but I still ignore all those stuffs.😢😢😢

有人又emo了，为什么呢？因为最近发生的那些吗…就忘了吧
是过去，是现在，是未来

Data Structure 15 动态查找表 BST & AVL

既支持查找操作，又支持增、删操作的集合称为动态查找表。
动态查找表抽象类可以这样定义：

template<class KEY,class OTHER>
class dynamicSearchTable{
    public:
        virtual SET<KEY,OTHER>* find(const KEY& x) == 0;
        virtual void insert(CONST SET<KEY,OTHER>&x) = 0;
        virtual void remove(const KEY& x) == 0;
        virtual ~dynamicSearchTable(){}
};

用于处理动态查找表的树称为查找树(Search Tree)。另一种动态查找表的实现是散列表，它是专用于集合查找的数据结构。

二叉查找树 Binary Search Tree

注：鉴于关于BST的实现已经在Introduction to Algorithm 2中实现了，这里只会简单说明一下一些要点

首先是存储：与普通二叉树的存储一样，只需存储二叉查找树的根结点
下面是一些运算实现：

• 查找：从根结点开始，决定是向左子树找还是向右子树找
• 插入：原则上必须保证插入一个结点后，这棵树仍是一棵二叉查找树；且在插入前需要进行查找操作以确保插入的元素不会重复
• （最复杂的操作）删除：如果删除的是叶结点，那么直接删除；如果删除的结点只有一侧存在结点，则那一侧的结点作为新的根结点；最复杂的是删除结点仍有2个子结点的情况，我们在右子树中找到最小的元素，为了避免大量数据元素的移动，我们选择将r的信息与这个最小的结点进行值交换，最小的那个结点成为了新的根结点，我们只需要在右子树中删除原有结点即可（划归到了1.2两种情况）

（老生常谈了）BST并不保证平衡，可能退化成链表，复杂度炸了

AVL树

注：鉴于关于AVL的思想已经在Introduction to Algorithm 3中介绍了(特别是证明树有对数级高度)

AVL树中每个结点的左右子树的高度最多差 1

首先还是存储上，AVL结点多了一个量用于记录结点高度
具体成员函数上，有抽象类规定的插入、删除和查找函数，除此之外，在私有成员函数中还包括了一组工具函数。包括调整树的平衡的adjust函数，四种旋转函数LL、RR、LR、RL，一个求树高度的height函数，清空AVL树的clear函数。

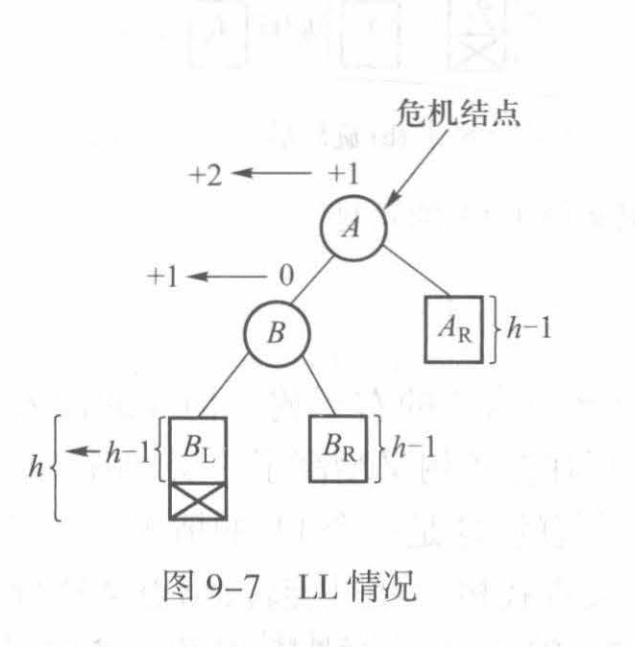
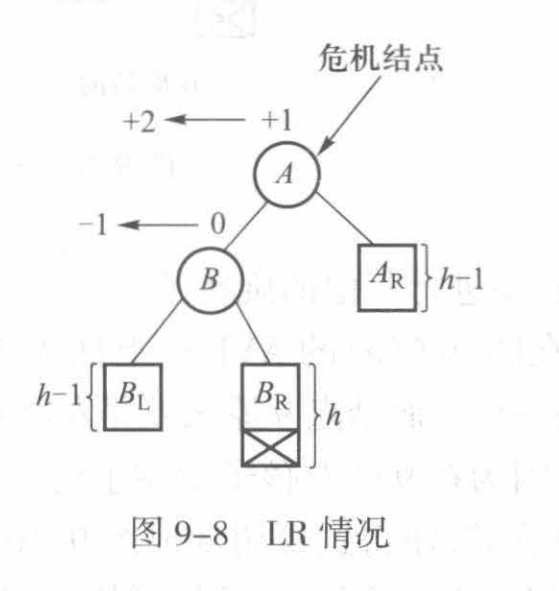
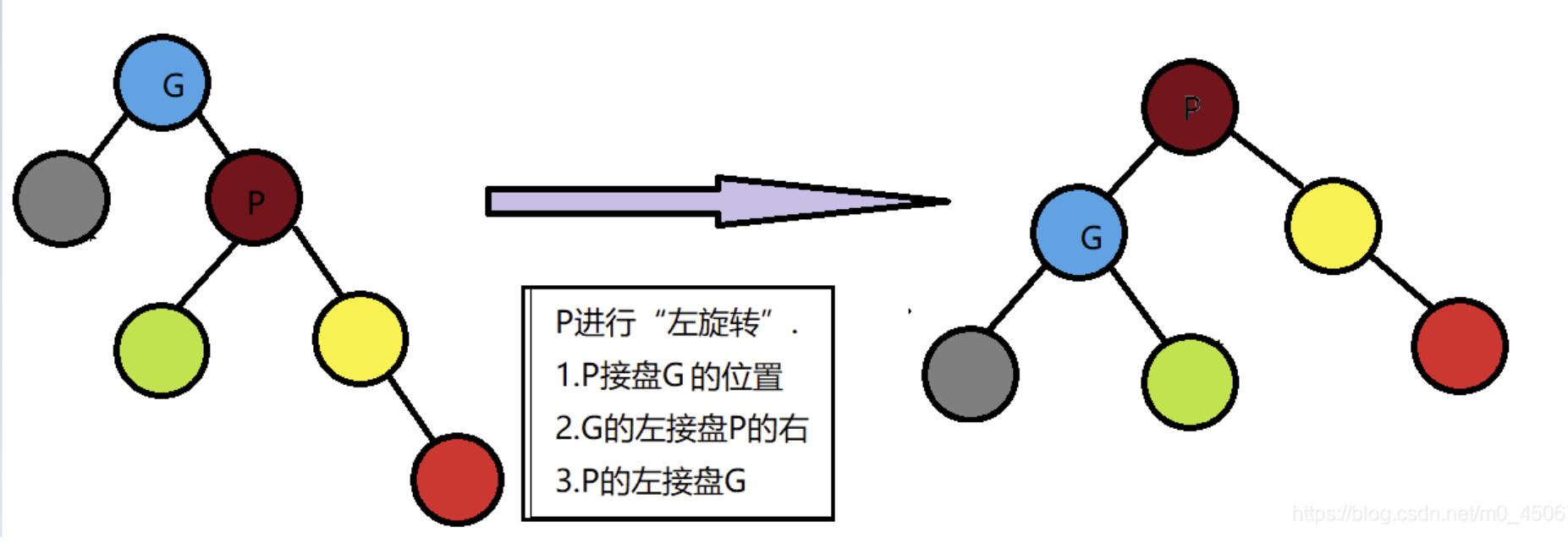
旋转rotate操作

具体来讲一讲AVL中一个特殊的操作：维护AVL的平衡。造成AVL失衡主要有四种情况：

首先，我们给出四种情形的示例图：

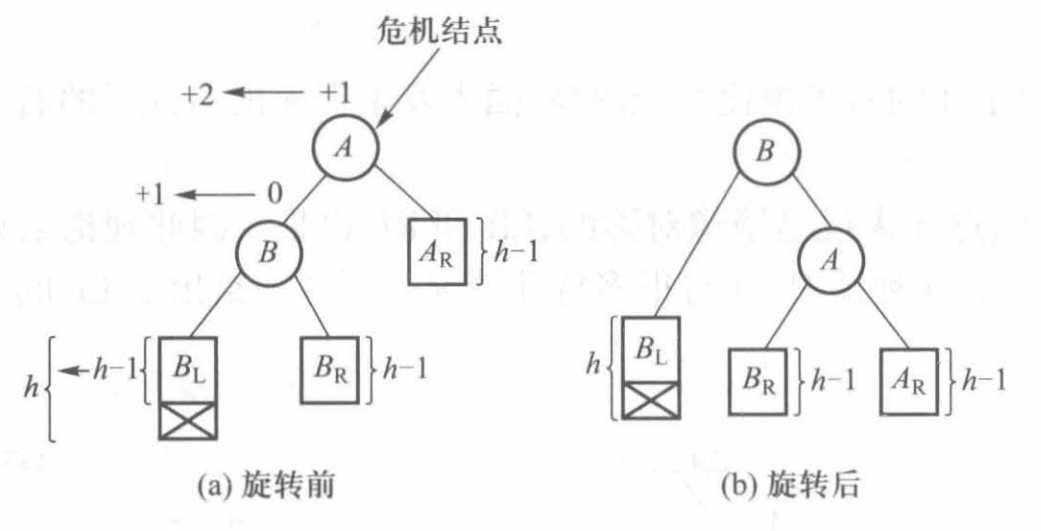
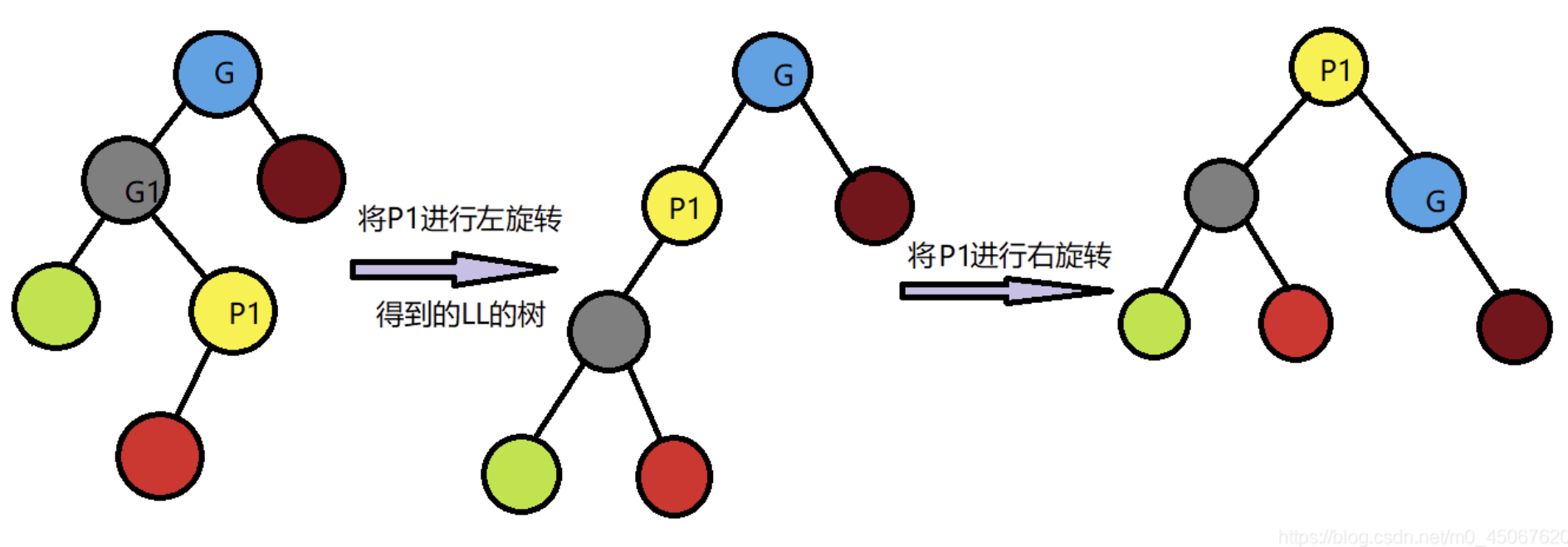
观察树可以发现，导致出现LL、RR型进行的插入操作发生在树的外部，可以通过单旋转调整好，而LR、RL型就复杂一些，插入操作发生在树的内部，需更复杂的双旋转操作。

不妨先看LL型：
插入前，结点A是平衡的，结点B原来的平衡度应该为0，否则A不会失去平衡或成为第一个失去平衡的结点。经过一次右旋的操作，树依然是有序的。如选图所示：

下面是代码实现（应该或许大概还是挺易懂的😢，虽然笨人已经被搞红温了）

template<class KEY,class OTHER>
void AVLTree<KEY,OTHER>::LL(Avlnode *&t){
    AVLnode *newRoot = t.left;
    t.left = newRoot.right;
    newRoot.right = t;
    t -> height = max(t -> left,t -> right) + 1;
    newRoot -> height = max(height(t),height(newRoot -> left)) + 1;
    t = newRoot;
}

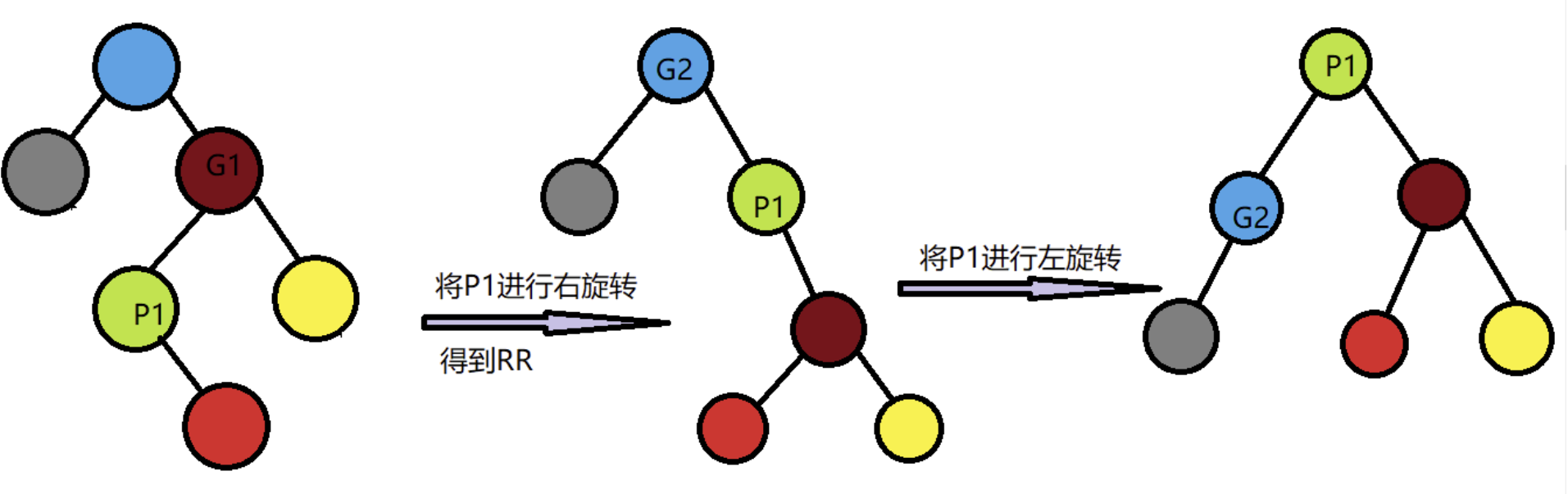
同理可以得到RR型，需要进行左旋操作，如下图所示：

下面是代码实现

template<class KEY,class OTHER>
void AVLTree<KEY,OTHER>::RR(Avlnode *&t){
    AVLnode *newRoot = t.right;
    t.right = newRoot.left;
    newRoot.left = t;
    t -> height = max(t -> left,t -> right) + 1;
    newRoot -> height = max(height(t),height(newRoot -> right)) + 1;
    t = newRoot;
}

LR、RL实际上是把LL、RR的操作进行复合
还是先来看一下过程吧，如图所示：

代码基于了LL、RR操作

template<class KEY,class OTHER>
void AVLTree<KEY,OTHER>::LR(Avlnode *&t){
    RR(t -> left);
    LL(t);
}

template<class KEY,class OTHER>
void AVLTree<KEY,OTHER>::RL(Avlnode *&t){
    LL(t -> right);
    RR(t);
}

To be honest：我觉得写成LL、RR、LR、RL的样子不是很直观，不如写成leftRotate、rightRotate、leftAndrightRotate、rightAndleftRotate，这样写至少能告诉我下面要进行怎样的操作。但单看怎么Rotate又不知道对应的哪种情况😇😇😇区别在于实现函数和调用函数的方便程度吧

插入insert操作（kind of a conclusion）

递归算法可能是实现AVL树插入的最简单的方法，要在AVL树T中插入一个键值为x的结点，可以递归地将它插入T的某棵合适的子树（记作T’），如果插入后T’的高度没有改变，就完成了操作。否则，根据x和T及T’中的键值选择单旋转或双旋转（以T为根），操作也结束了。

与二叉查找树一样，插入操作也是通过递归实现的。如果树是空树，将结点插入为根结点，递归结束。如果插入结点比根结点小，则在左子树上插入。如果插入结点比根结点大，则在右子树上插入。只是AVL树还要多做一件事，就是在插入后要检查从插入结点到根结点的路径上有没有结点失衡。如果有，则作相应的调整。从插入结点到根结点的回溯过程由递归函数自动完成，在递归调用返回后检查根结点的平衡度。

template<class KEY,class OTHER>
void AVLTree<KEY,OTHER>::insert(const SET<KEY,OTHER>&x){
    insert(x,root);
}

template<class KEY,class OTHER>
void AVLTree<KEY,OTHER>::insert(const SET<KEY,OTHER>&x,AvlNode *&t){
    if(t == nullptr){
        t = new AVLNode(x,nullptr,nullptr);
    }else if(x.key < t -> data.key){
        insert(x,t -> left);
        if(height(t -> left) - height(t -> right) == 2){
            if(x.key < t -> left -> data.key){
                LL(t);
            }else{
                LR(t);
            }
        }
    }else if(x.key > t -> data.key){
        insert(x,t -> right);
        if(height(t -> right) - height(t -> left) == 2){
            if(x.key > t -> right -> data.key){
                RR(t);
            }else{
                LR(t);
            }
        }
    }
    t -> height = max(height(t -> left),height(t -> right)) + 1;
}

这还是比较容易的😋😋😋至多只需要调整一个结点

删除remove操作

两步操作：

• 删除结点 x（与BST一样）
• 调整平衡

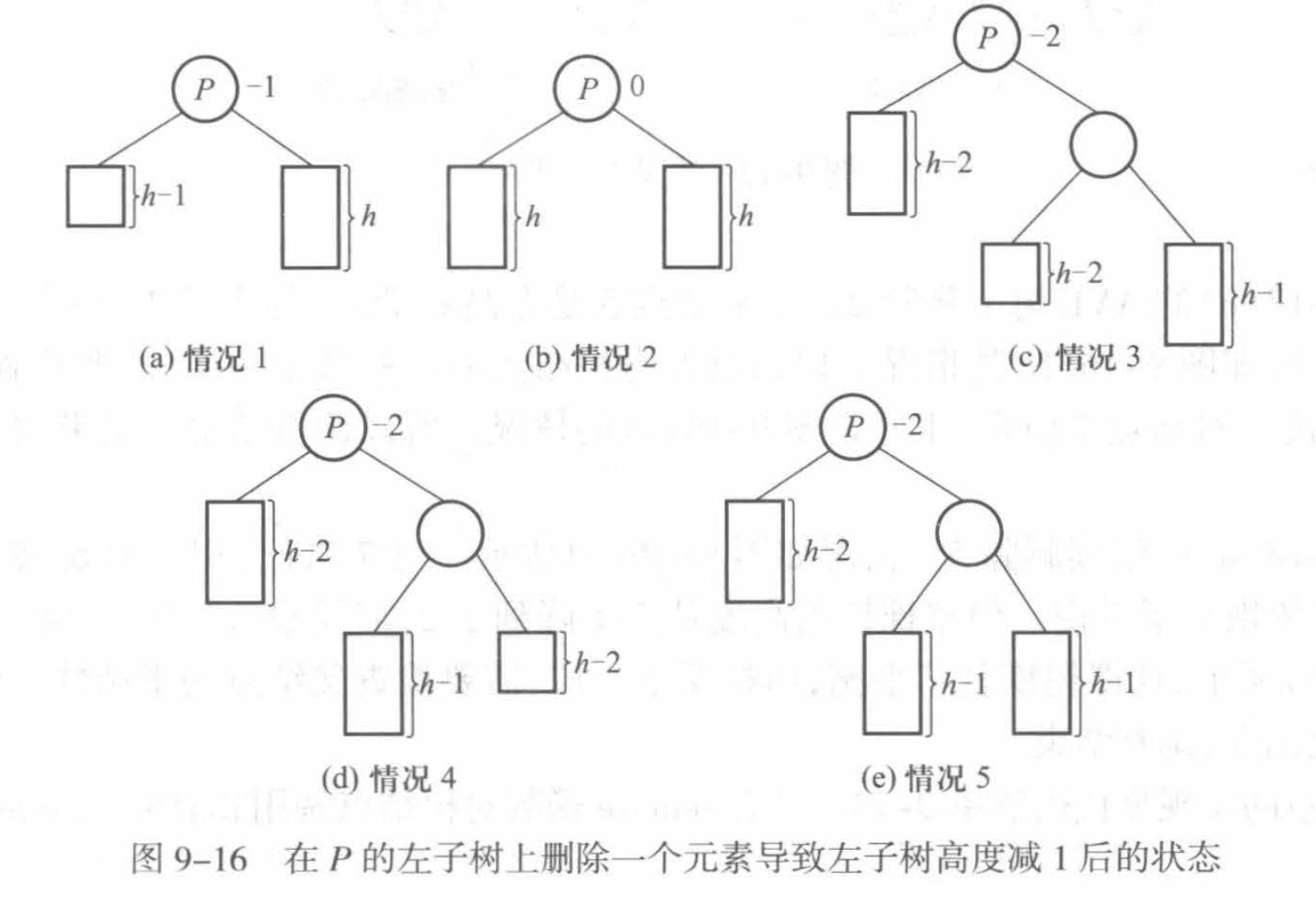
删除操作没有插入操作那么幸运，调整可能导致整棵子树高度下降，从而影响该子树的父结点的平衡度。只有当某个结点的高度在删除前后保持不变，才无须继续调整。
下面是代码实现：

template<class KEY,class OTHER>
void AVLTree<KEY,OTHER>::remove(const KEY &x){
    remove(x,root);
}

template<class KEY,class OTHER>
bool AVLTree<KEY,OTHER>::remove(const KEY &x,Avlnode* &t){
    if(t == nullptr){
        return true;
    }
    if(x == t -> data.key){
        if(t -> left == nullptr || t -> right == nullptr){
            AVLnode *oldNode = t;
            if(t -> left == nullptr){
                t = t -> right;
            }else{
                t = t -> left;
            }
            delete oldNode;
            return false;
        }
        AVLNode *tmp = t -> right;
        while(tmp -> left != nullptr){
            tmp = tmp -> left;
        }
        t -> data = tmp -> data;
        if(remove(tmp -> data,t -> right)){  //若树不会变矮
            return true;
        } 
        return adjust(t,1); //1表示调整右子树
    }else if(x < t -> data.key){
        if(remove(x,t -> left)){
            return true;
        }
        return adjust(t,0);
    }else if(x > t -> data.key){
        if(remove(x,t -> right)){
            return true;
        }
        return adjust(t,1);
    }
}

//返回值为true即说明高度没变，无需进一步检查平衡，反之，则需要进一步检查
template<class KEY,class OTHER>
bool AVLTree<KEY,OTHER>::adjust(AVLnode *& t,int subtree){
    if(subtree){  //在右子树上删除，使右子树变矮
        if(height(t -> left) - height(t -> right) == 1){
            return true;
        }
        if(height(t -> left) == height(t -> right)){
            -- t -> height;
            return false;
        }
        if(height(t -> left -> left) < height(t -> left -> right)){
            LR(t);
            return false;
        }
        LL(t);
        if(height(t -> left) == height(t -> right)){
            return false;
        }else{
            return true;
        }
    }else{ //在左子树上删除，使左子树变矮
        if(height(t -> right) - height(t -> left) == 1){
            return true;
        }
        if(height(t -> left) == height(t -> right)){
            -- t -> height;
            return false;
        }
        if(height(t -> right -> left) > height(t -> right -> right)){
            RL(t);
            return false;
        }
        RR(t);
        if(height(t -> left) == height(t -> right)){
            return false;
        }else{
            return true;
        }
    }
}

Reference

• AVL树的旋转图解和简单实现
• 二叉平衡(AVL)树中的 LL旋转、RR旋转、LR旋转、RL旋转 的详细解释