Mathematical-Logic3

Before：下课就去捞！3周没捞了😋😋😋上大学后捞的频率大幅增长🤣🤣🤣

🐖🐖🐖

Mathematical Logic 3 重合引理 同构引理

概念回顾

项是由变量、常量符号和函数符号通过递归方式构造的表达式。
公式（formula）是由项通过谓词符号、逻辑连接词和量词构造的表达式。
结构由域和解释函数组成。
解释由结构和赋值函数（将自由变量映射到域中的元素）组成。

• 原子公式：包括等式公式、谓词公式R
• 逻辑连接词：¬、∧、∨、→、↔
• 量词：∀xφ (x是变量，φ 是公式)、∃xφ (x是变量，φ 是公式)

我们可以解释term、解释formula、解释sentence

结构归纳法（对公式进行归纳）

公式的归纳基于公式的结构，即公式的构造方式。由于公式是通过递归方式定义的（从原子公式逐步构造出复杂公式），因此我们可以使用结构归纳法来证明公式的性质。
公式的归纳证明通常分为以下几个步骤：

• 证明性质𝑃对所有原子公式成立
• 归纳步骤：假设性质𝑃对某些公式𝜑和𝜓成立（归纳假设），然后证明𝑃对通过这些公式构造的复杂公式也成立。

重合引理（The Coincidence Lemma）

设I1(A1,β1),I2(A2,β2)是2个S-解释，且满足以下条件：

• A1 = A2（解释的域相同）
• 对于S：= S1 ∩ S2中的每个符号，它们在A1、A2中的解释相同

那么：

• 对于任何S项t，如果β1(x) = β2(x)对于t中的所有变量x成立，则I1(x) = I2(x)
  即需要满足结构的解释相同和变量的赋值相同
• 对于任何S公式𝜑，如果β1(x) = β2(x)对于𝜑中的所有自由变量x成立，则I1 |= 𝜑 当且仅当 I2 |= 𝜑
  即需要满足结构的解释相同和自由变量的赋值相同

证明依赖于结构归纳法

同构引理（The Isomorphism Lemma）

首先给出同构的定义：
在模型论中，同构是指两个结构之间存在一个双射（bijection），这个双射保持了结构中的所有关系、函数和常量。
具体来说：
设A(A,I)和B(B,J)是2个S—结构，其中A和B是它们的域，I和J是解释函数。
一个同构𝜋：A → B是一个双射，满足以下条件：

• 保持关系
  
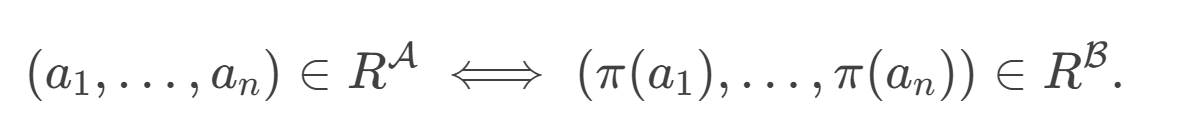
• 保持运算
  
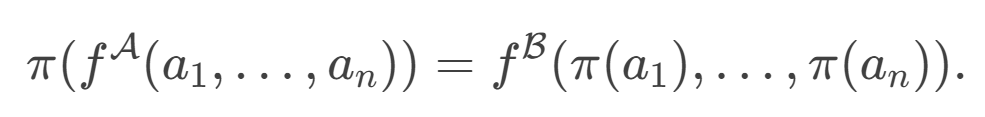
• 保持常量
  

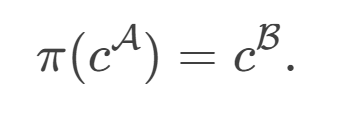
如果存在这样的双射𝜋，则称结构A和B是同构的，记作A≅B
例子：群论 & 图论中的同构

同构的性质：

• 自反性（Reflexivity）：A ≅ A
• 对称性（Symmetry）：若A ≅ B，则B ≅ A
• 传递性（Transitivity）：若A ≅ B 且 B ≅ C ，则A ≅ C

因此，同构是一个等价关系

那么同构引理可以表示为：
如果A、B是两个同构的S-结构，则对于任何S-句子𝜑，有
A |= 𝜑 ⟺ B |= 𝜑
这意味着，同构的结构在一阶逻辑中无法被区分，它们满足相同的句子。