Mathematical-Logic4

Before：昨天立的flag要在这周结束前finish map，经过昨天一下午+一晚上和今天一上午+一下午艰难地debug（快被leak卡死了呜呜呜），终于过啦！至此，STLite-2025这个轻量级STL库的大作业全部完成🥳🥳🥳比ddl提前了一整个月，本学期只剩下最后一个大作业——Ticket System了，所以：现在可以美美开始BPT啦（bushi）but，数理逻辑还是好抽象啊😣😣😣鼠鼠菜菜

今天是3月14日，𝜋节。2022.03.14 - 2025.03.14，整整三年了，还是没放下，要带着遗憾一直到老了…忽远忽近，忽明忽暗。过去那么久了，还是忘不了。永远是我的青春，祝你一路顺风。

Mathematical Logic 4 同构引理的证明 & 替换

Call back previous 一阶逻辑语义

同构
存在一个A -> B 的映射满足：

1. 是双摄
2. 保持关系（n元关系运算符）
3. 保持运算（n元函数运算符）
4. 保持常量（常数c）

则结构A、结构B同构

在上周的作业中，我们证明了同构是一种等价关系。回忆，等价关系需要满足三个条件：

1. 自反性
2. 对称性
3. 传递性

同构引理的证明

Recall:
A、B是2个同构的S-结构，那么对于所有S-sentence 𝜑，有：

A |= 𝜑 ⟺ B |= 𝜑

Prof:
由重合引理可知：
A |= 𝜑 ⟺ (A,β) |= 𝜑
B |= 𝜑 ⟺ (B,β’) |= 𝜑

so A |= 𝜑 ⟺ B |= 𝜑 ⟺ (A,β) |= 𝜑 ⟺ (B,β’) |= 𝜑

定义β^𝜋(x) := 𝜋(β(x))
那么我们要证：
(A,β) |= 𝜑 ⟺ (B,β^𝜋) |= 𝜑 (𝜑 是任意S-公式)
// 这不就从句子推广到公式上了嘛

也就是要证明：
I:= (A,β) I^𝜋:= (B,β^𝜋)
𝜋(I(t)) = I^𝜋(t)

这里改写成解释，也就可以进行结构归纳法（对公式的归纳了）
略

项的替换 Substitution

设t 是一个S-term，x0,…,xr是变量，且t0,…,tr是S-terms。那么我们可以这样定义项的替换：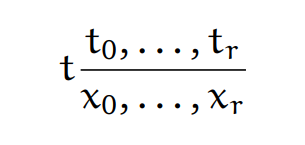

(a)如果t = x是一个变量，那么：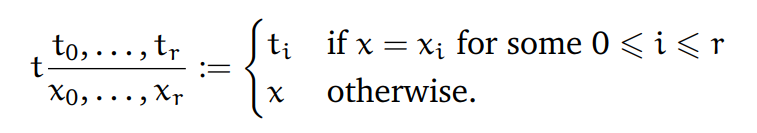

(b)如果t = c是一个常数，那么：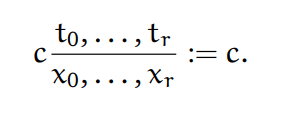

(c)对于一个函数项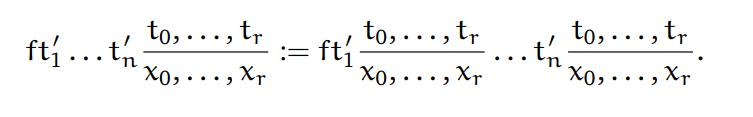

公式上的替换

设𝜑 是一个S-formula，x0,…,xr是变量，且t0,…,tr是S-terms。那么我们可以这样定义：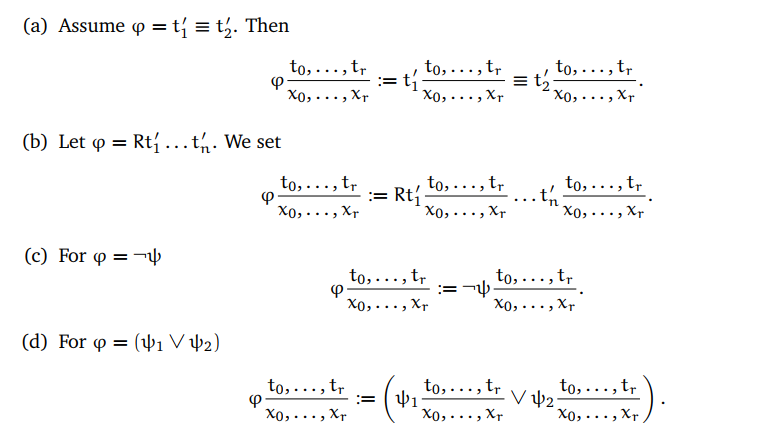

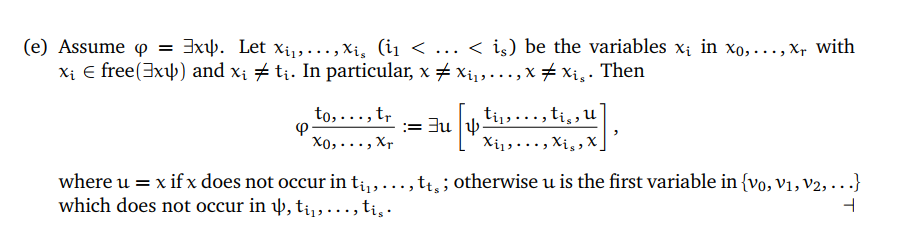
赋值上的替换（对于自由变量）

替换引理

替换引理分为2个部分：

项的替换引理

对一个项 𝑡 进行替换后，其解释等于在原解释 𝐼 的基础上，将变量x0,…,xr替换为项t0,…,tr的解释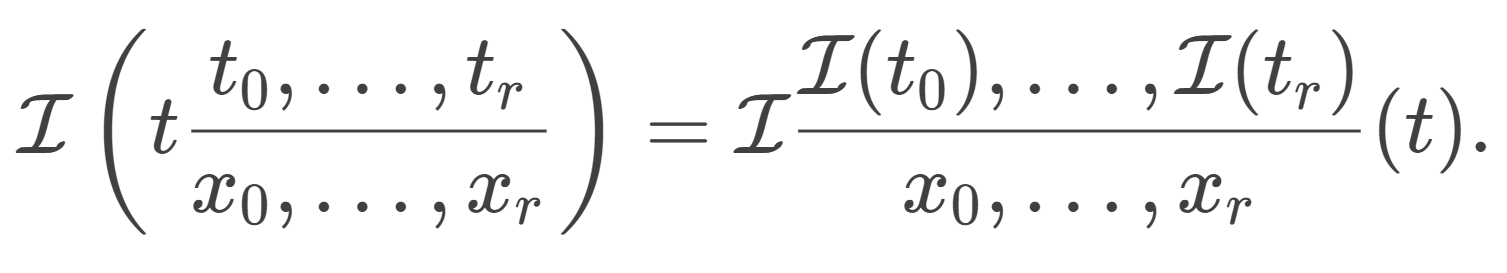

公式的替换引理

对一个公式 𝜑 进行替换后，其真值等于在原解释 𝐼 的基础上，将变量x0,…,xr替换为项t0,…,tr的解释后的真值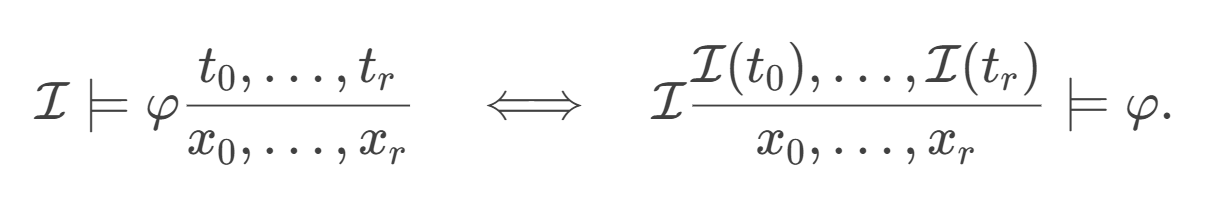

二者均为语法替换 ⟺ 语义更新