Data-Structure16
Before:2023.12.31——2025.03.15,440天后,又在影院与LaLaLand重逢。2023.12.31,上完了最后一节课,惆怅,迷茫,又适逢LaLaLand重映,第一次在影院看了(以前在家看过不少遍)。我承认,就连23年的年终总结有近一半也与这个我未曾谋面的人有关。在那个时间点看LaLaLand真的让我很久都没有释怀,也曾有过很多冲动的想法,不想高考,想飞去Melbourne,想去曾经学在的Berkeley,CA。这是我第一次将这件事说出来,那段懵懂的喜欢就像LA傍晚的天空那样,是浪漫的紫色。说不清楚讲不明白,我到底是曾经喜欢过,还只是向往一段Mia和Seb的爱情与梦想,甚至说只是想去一次LA吧。LA可能是我除了南京、上海之外最熟悉的城市了(虽然从未去过)。幻想过格里菲斯天文台的浪漫,比弗利山庄的纸醉金迷,SantaMonica的热情…也幻想着天使之城有像Seb那样执着于理想的年轻钢琴家,契合的灵魂,在蓝调的格里菲斯公园共舞…我的vx、github头像一直是灯光下Seb的演奏,可能我喜欢的人,是Seb那样的吧。依然是久久不能平复。曾一次又一次地告诉自己,坦然接受生命中的失去与遗憾,却发现风起时,意难平。或许最遗憾的是,不会钢琴吧…
City of star Are you shining just for me
And you will be all right.
记得高三的时候看过wxl的一篇作文,写的是爱乐之城中红与蓝的色调,好像还挺契合今天红黑树的主题的😢叫红蓝树也未尝不可,反正都是RBT
Data Structure 16 红黑树
首先声明一下,鉴于本人已经通过了map大作业的AVL实现(就是炫耀,盐都不盐了🤣😉),且RBT是A班的要求,与我无关,故我不会对RBT进行详细的代码实现,更侧重于操作的思想
红黑树定义
一种平衡树,常用来替换 AVL ,时间代价同样是O(logN)的。它是一棵具有下列特点的二叉查找树:
(1)每个结点被染成红色或黑色
(2)根结点是黑色的
(3)如果一个结点是红色的,那么它的儿子结点必须是黑色的。
(4)从任何一个结点出发到空结点(即空指针指向的结点)的路径上,必须包含相同数量的黑色结点。
从红黑树的定义可知,红黑树是比 AVL 树平衡性更弱的平衡树(AVL树具有严格平衡性,所以在查找操作的时间性能上要优于RBT)。在任何一条路径上不能有两个连续的红结点。因此,在每条路径上红结点的个数都是有限的。也就是说,各条路径的长度差是有限的。最长的路径是最短路径的2倍。
下图是一棵红黑树: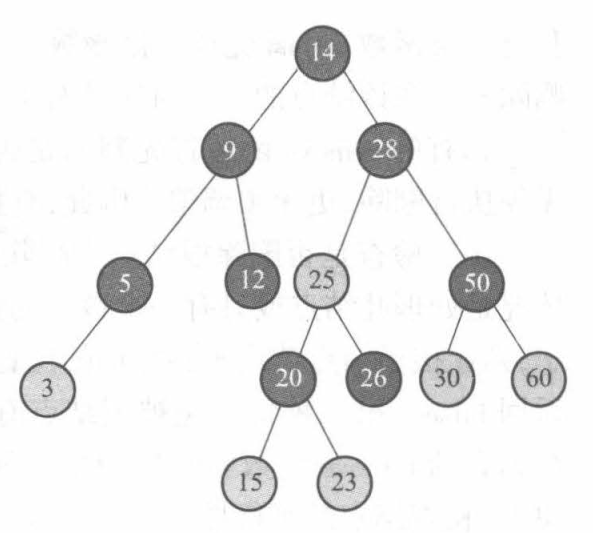
而这就不是红黑树了: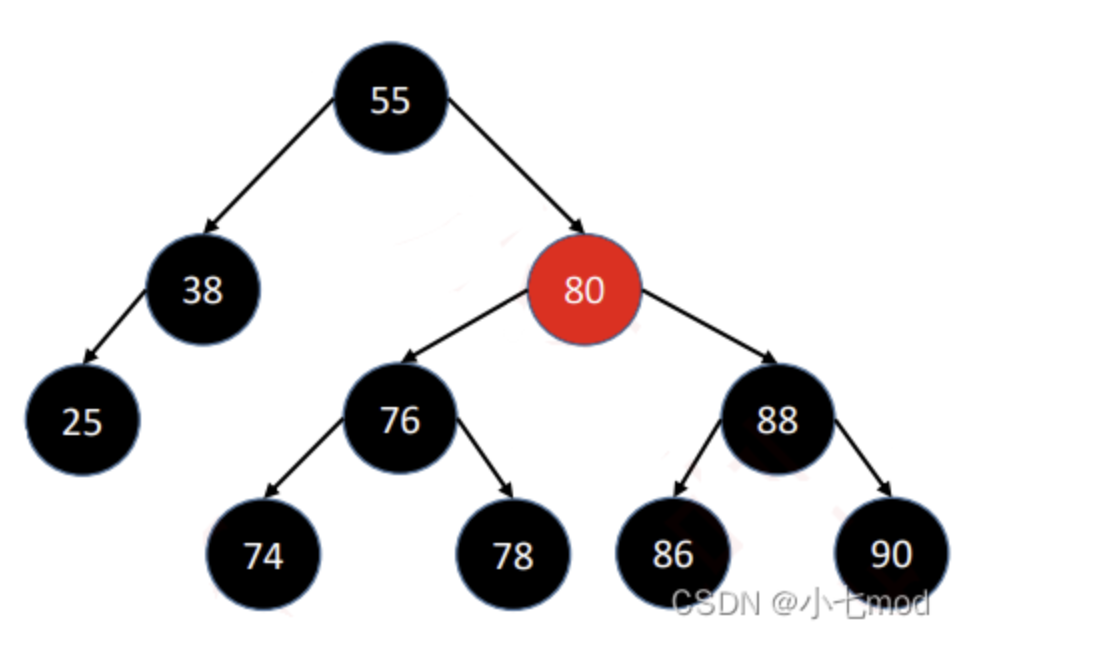
我们容易通过数学归纳的方法得到,对于一棵有N个结点的红黑树,其高度最多为2log(N + 1)。这里Call back一下AVL的高度最多为1.44logN,还是要略好一些的😝
红黑树的存储实现
相较于先前写过的BST、AVL,RBT结点多了一个枚举类型colorType,用于记录该点的颜色。但与BST、AVL不同的是,在BST、AVL中,我们采用了递归的方式来实现insert、remove等操作,所以insert、remove等拥有私有成员函数,但是红黑树的insert、remove操作采用非递归的方式实现,不需要私有成员函数了。
红黑树的插入实现
红黑树的插入操作
如果将新结点着色为黑色,那么将违背红黑树的性质4,因为这将导致从根结点到插入结点的路径上的黑结点个数比其他路径上的黑结点个数多。因此,只能将新插入的结点着色为红色。如果新插入结点的父结点是黑色的,则平衡没有被破坏,整个插入过程结束。但如果新插入的结点的父结点是红色的,就将出现连续的红结点,这将违背红黑树的性质3。为解决这个问题,基本的方法是修改结点的着色和旋转。
红黑树的旋转操作
分为2种情况:
1.父结点 P 的兄弟结点 S 是黑色的(一红一黑)
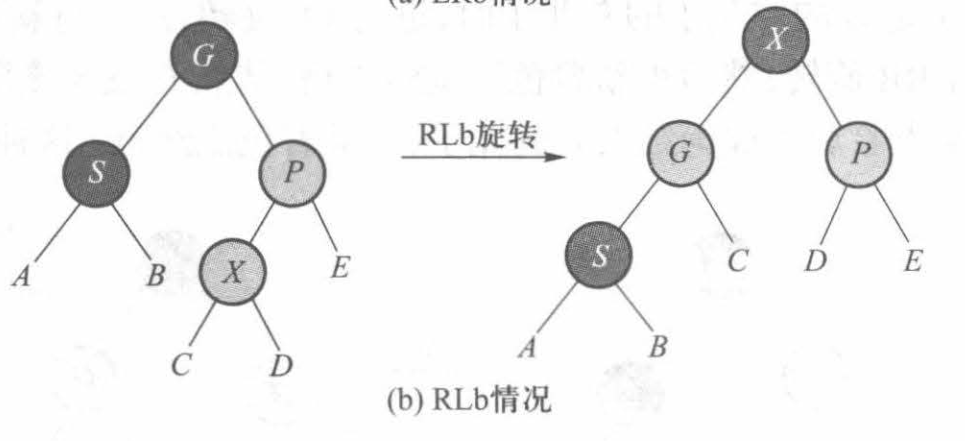
(1)插入结点是外侧结点
我们进行LLb或RRb旋转,如下图所示: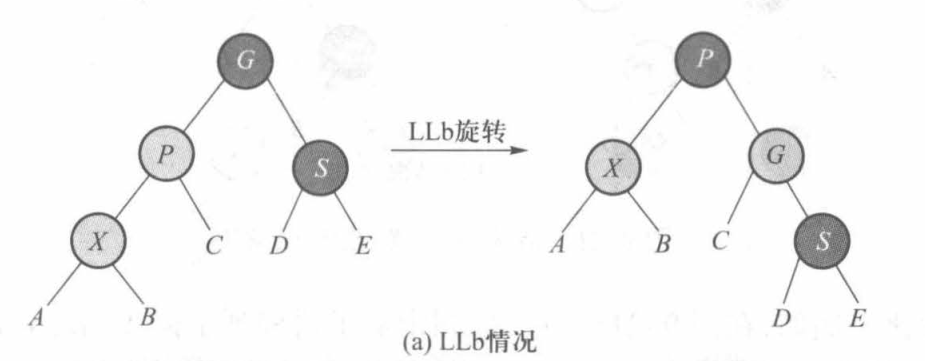
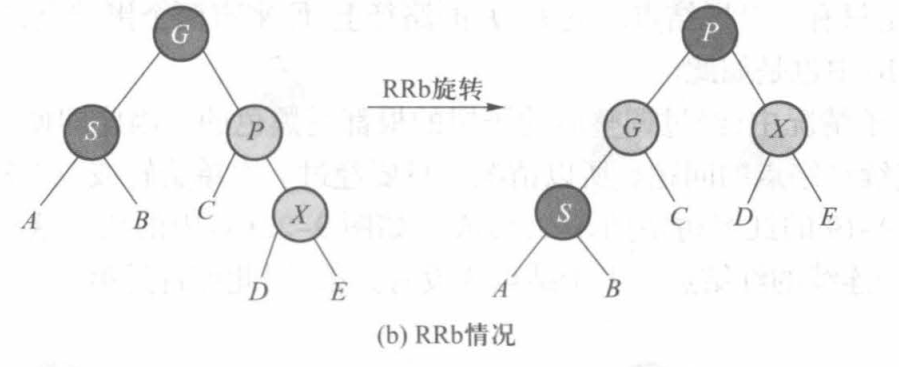
省流:其实就是AVL的旋转 LL or RR + 颜色调整
(2)插入结点是内侧结点
我们进行LRb或RLb旋转,如下图所示: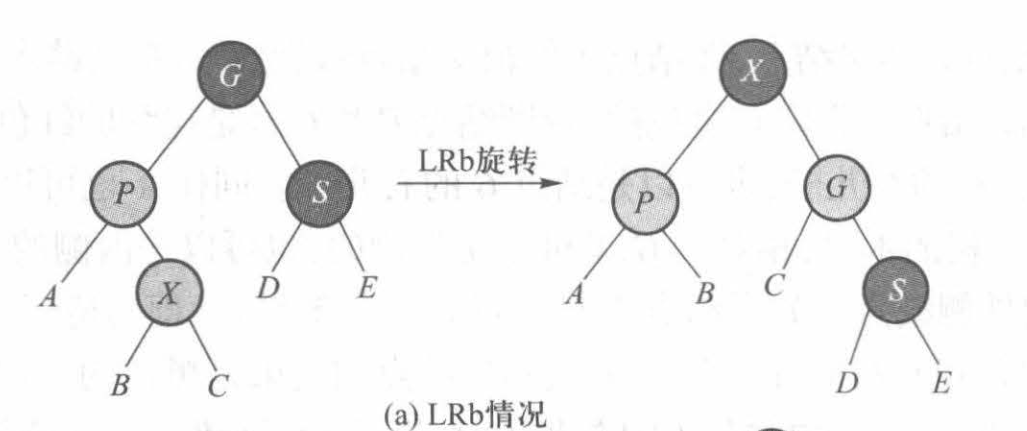
省流:其实就是AVL的旋转 LR or RL + 颜色调整
2.父结点 P 的兄弟结点 S 是红色的(两红)
这种情况的处理真妙!用不着什么旋转,只要把这对双红兄弟变成双黑,把根结点变成红色即可,维护了性质4,如下图所示: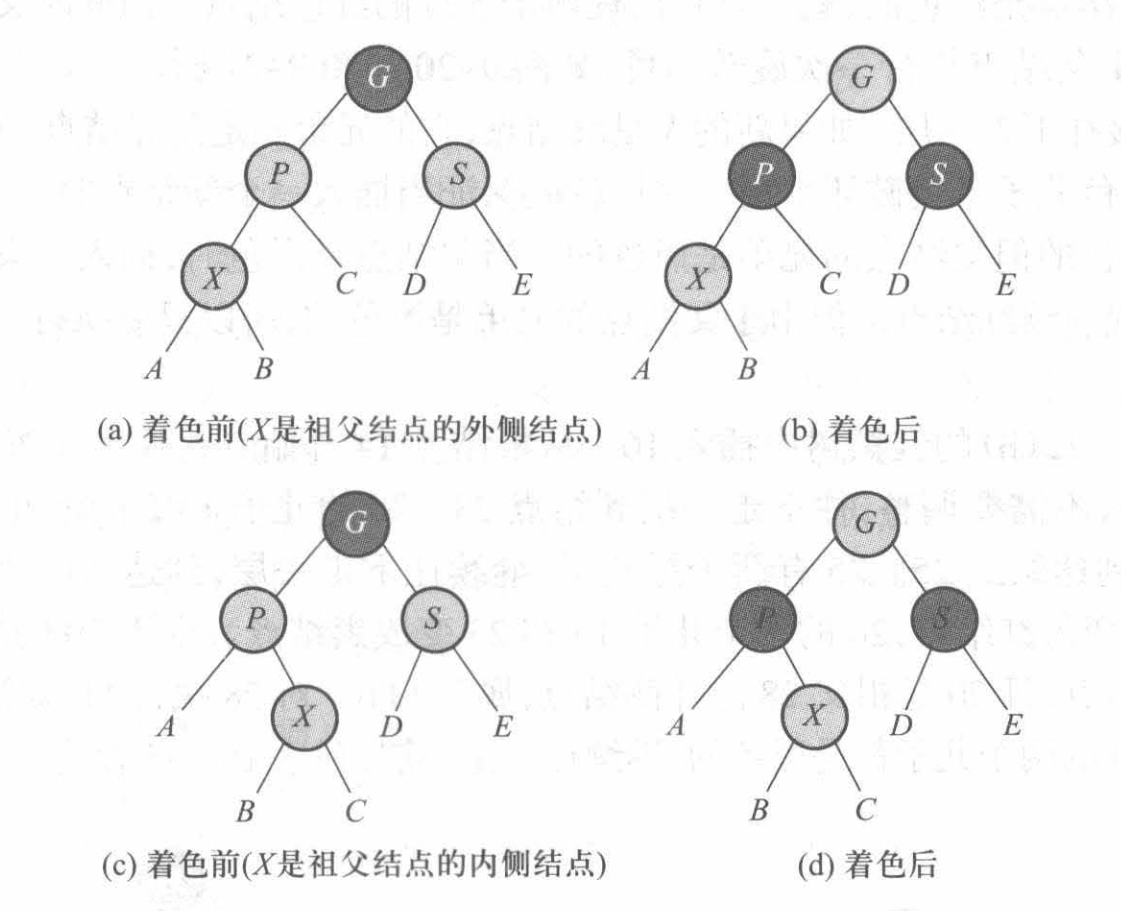
but:真的有这么容易吗?注意到根结点成了红色,但如果根结点的父亲也是红色呢?那就与性质3相违背了,所以我们还需要向上调整,最坏可能会到根
红黑树好在哪儿😅
目前的感觉是不仅树比AVL高,还比AVL难写(幸好不用写🤣)
但其实,优势其实在调整上。写完AVL其实不难发现,插入删除很容易就会让某个根结点失去平衡性,需要多次的调整,往往还不是一次调整可以结束的,需要不断递归向上。但是红黑树有1/2的情况是无需调整的(对应根结点为黑色),剩余1/2的操作,涉及旋转的只需进行一次调整,而重新着色的有1/2的概率只进行一次操作,剩下的向上调整其实概率已经很小了。且又递归地每上一层概率更小,因此,红黑树在维护平衡性方面时间性能相当不错。
这大概就是 Java 中的 TreeMap、JDK 1.8 中的 HashMap、C++ STL 中的 map 均是基于红黑树结构实现的原因吧。
红黑树的删除实现
删除操作首先使用普通的二叉查找树的删除算法删除结点,然后进行旋转及颜色的调整。BST的删除最终可以归结到2种情况:删除叶结点和删除只有一个儿子的结点。我们只需解决这两种情况下的着色问题。
如果被删结点是红色的,删除操作结束,因为并未引起红黑树性质的改变。但是,若被删结点是黑色的,将会引起和该结点相关的路径上的黑色结点数量的减少,从而不满足红黑树的性质4。
从这里可以得到一个启发:如果能够保证被删结点是红色叶结点,就可以简化删除操作。那么如何做到这一点呢?
设结点X是所遇到的当前结点,T是它的兄弟结点,而结点P是它们的父结点。对每个遇到的X,都试图把它变成红色。当最后遇到被删结点时,由于它是红色的叶结点,可以直接删除。
在自根向下的搜索过程中,当搜索到一个新结点时,可以确信其父结点P是红色的,而结点X和T是黑色的(因为不可能有两个连续的红色结点存在)。根据X的颜色,可以分成两种情况。
下面进行分类讨论:
1.结点 X 有两个黑色儿子 意味着结点X可以放心地变红
(1)T 有两个黑色儿子,调整颜色,将 P 变成黑色, X 和 T 变成红色,如下图所示: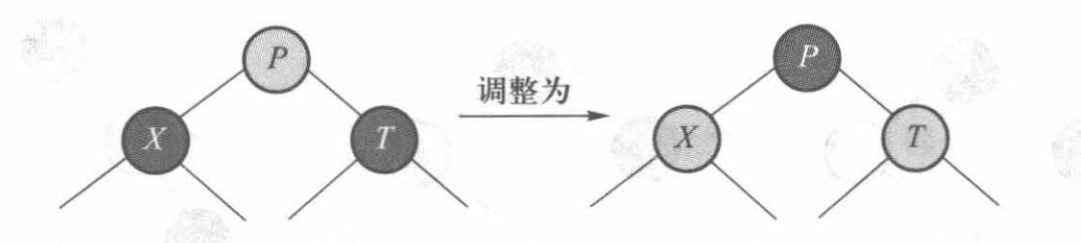
(2)T 有一个外侧的红色儿子,让 T 和 P 进行一次单旋转,并重新着色,如下图所示: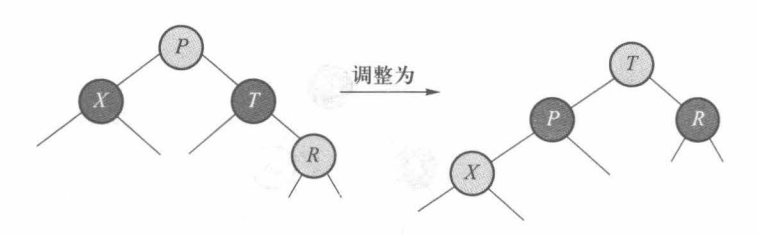
(3)T 有一个内侧的红色儿子,对 P 执行一次双旋转,让 T 的红儿子旋转到 P ,并重新着色,如下图所示: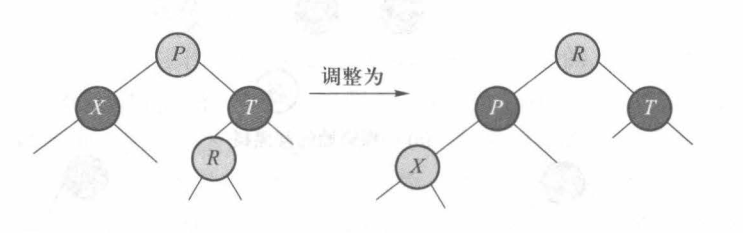
注意:如果T有2个红色儿子,那么单旋双旋均可(显然单旋简单一些)
2.结点 X 至少有一个儿子是红色的
如果 X 不是被删结点:
可以继续前进到下一层。
(1)幸运的话,“前进”一层之后,新的 X 正好就是红色结点😋,回归到情况一,问题就解决了,这大概有一半的可能性。 (走向红色)
(2)否则,当前结点 X 是黑色的(走向黑色),结点 T 是红色的,父结点 P 是黑色的,如下图所示: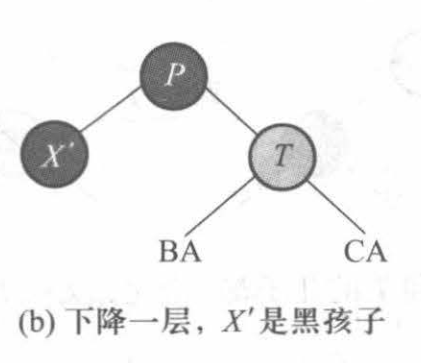
进行一次旋转: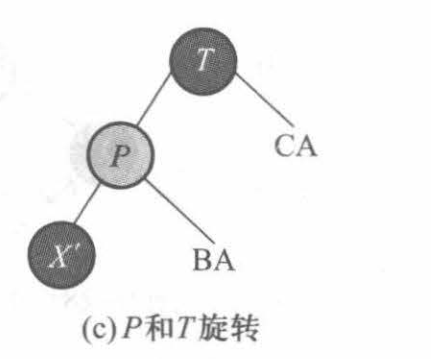
由于旋转后结点 X 仍然不是红色的,但父结点已经是红色的,即转换为情况一,按情况一继续调整结点 X 的颜色。
如果X不巧就是被删结点(且有2个儿子)
(1)有2个儿子
此时将在右子树上寻找“替身”。如果 X 的右孩子是红结点,无须调整,直接沿右孩子往下走一层。否则左孩子一定是个红结点。对 X 执行一次 LL 旋转使 X 变成红色。
(2)只有1个儿子
则该孩子必为红结点,将 X 与孩子结点做一个单旋转。此时 X 变成了红结点。
Conclusion
其实我删除操作有一小部分并不是很理解,但已经深切地认识到RBT的调整着色的思想,且RBT调整的次数确实要小于AVL,性能上有一定的优越性。但是insert操作应该能写出来,remove是真的难写啊!(相较之下AVL的remove操作已经好写很多了)