Data-Structure17

Before：感觉红黑树的实现好困难啊，即便是学完了一遍有些删除操作的细节都没有特别搞懂，感觉是一个实现和理解上都相当有难度的数据结构。今天要讲的是红黑树的一种特殊情况——AA树，希望会简单一点？（毕竟是B班写的呜呜呜）

Data Structure 17 AA树

AA树的定义

开幕雷击：《一种简单但却很有竞争力的平衡查找树》
好好好！

AA树是一类特殊的红黑树，它对红黑树增加了一个限制条件：左儿子不能为红色。
所以一棵AA树需要满足如下条件：

1. 每个节点都可以是红色或黑色。
2. 根节点总是黑色。
3. 叶节点（NULL）总是黑色。
4. 红色节点的两个子节点必须都是黑色，即没有两个相邻的红色节点。
5. 从根节点到 NULL 节点的每条路径都有相同数量的黑色节点。
6. 红色节点只能作为右子节点。

为了更进一步简化实现，可以用一种更直接的方法来表示平衡信息，即采用结点的层次，而不是结点的颜色。 所谓的结点层次就是结点到空结点的路径上左链的数量。
so，你自然会发现，AATree类中不再有枚举类型colorType了（欢呼.jpg）
如果把结构上的要求由颜色转为层次表示，左儿子肯定比它的父亲低1个层次，右儿子可能比父亲的层次低0或1层（右儿子可红可黑）。
将层次的概念的概念用图的方式表示就形成了水平链表示法。水平链连接层次相同的父子结点。下图就是一棵简单的AA树的水平链表示：

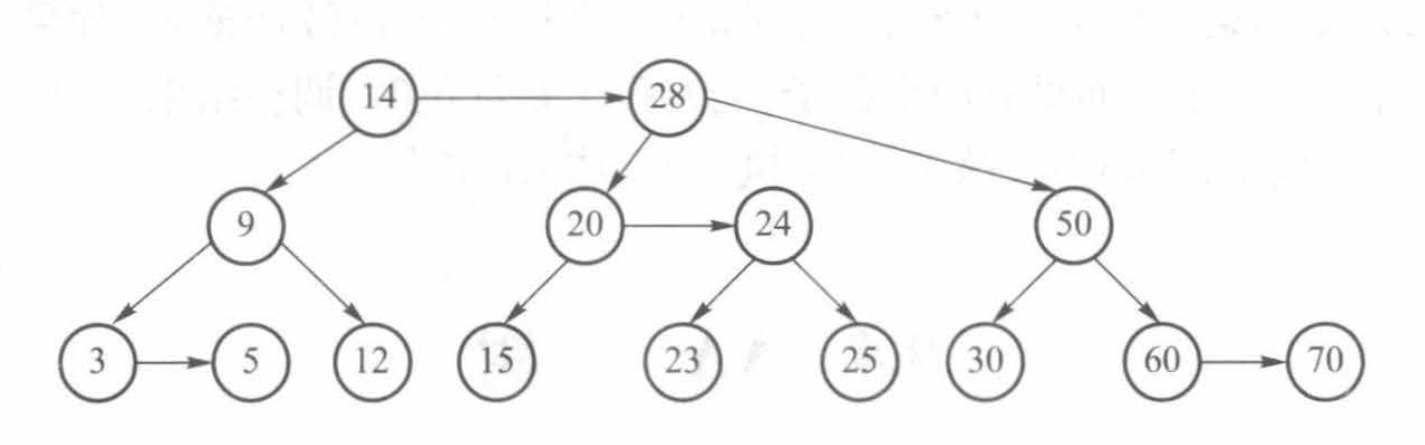
这张可能更好看一些？

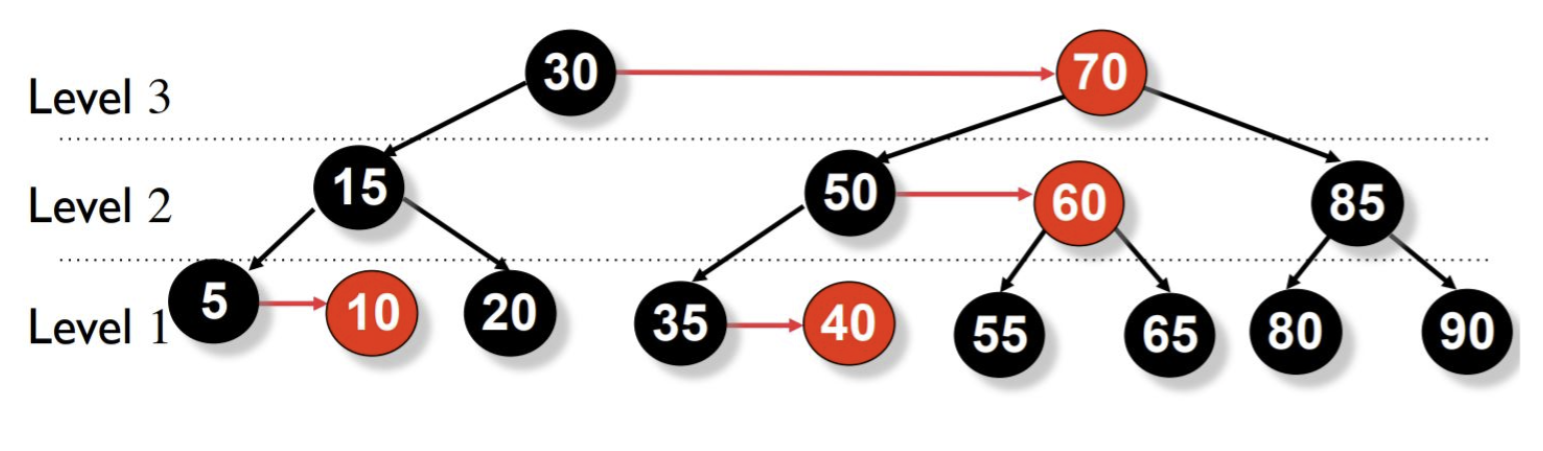
允许单独的右水平链接，但不允许连续的右水平链接；不允许左水平链接。

AA树的存储实现

由于AA树的平衡信息用层次表示，所以结点层次是一个成员变量。

template<class KEY,class OTHER>
class AATree:public dynamicSearchTable<KEY,OTHER>{
    struct AANode{
        SET<KEY,OTHER> data;
        AANode *left;
        AANode *right;
        int level; //结点层次

        AANode(const SET<KEY,OTHER> &d,AANode *l = nullptr,AANode *r = nullptr,int lv = 1):data(d),left(l),right(r),level(lv){}
    };
    AANode *root;

public:
    AATree():root(nullptr){}
    ~AATree() {
        makeEmpty(root);
    }
    SET<KEY,OTHER> *find(const KEY &x)const;
    void insert(const SET<KEY,OTHER> &x) {
        insert(x,root);
    }
    void remove(const KEY &k) {
        remove(k,root);
    }

private:
    void insert(const SET<KEY,OTHER> &x,AANode *&t);
    void remove(const KEY &k,AANode *&t);
    void makeEmpty(AANode *&t);
    void LL(AANode *&t);
    void RR(AANode *&t);
    int min(int a,int b) {
        if(a < b) {
            return a;
        }else {
            return b;
        }
    }
};

AA树的运算实现

AA树的查找和删除操作和RBT、AVL、BST均相同，不做实现了😢😉重点还是插入和删除操作

AA树的插入操作

与红黑树相同，新的数据元素总是插入为红色结点，但这可能会导致水平左链和连续水平右链的出现，显然与AA树的要求不符。
但无论哪种情况，都可以通过一次单旋转解决问题。如下图所示的两种情况：

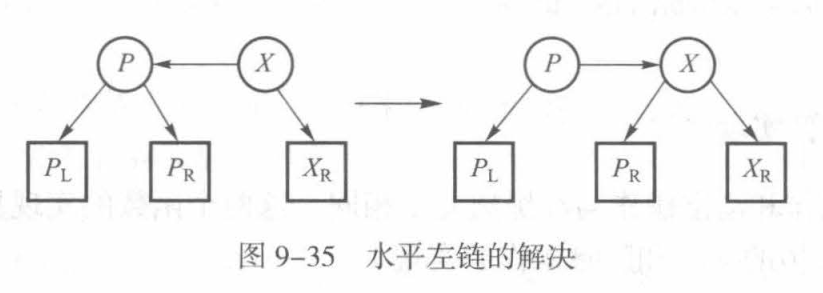
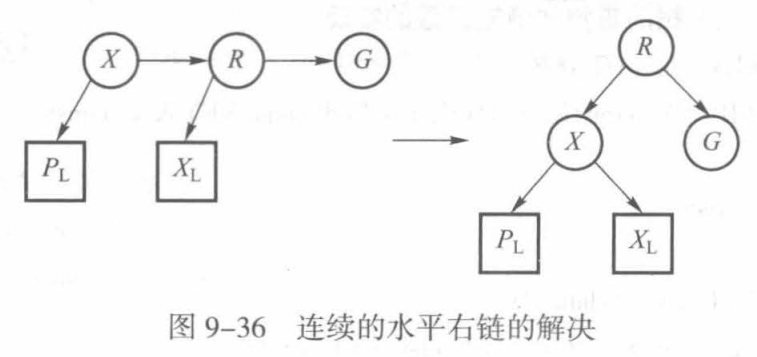
我还是喜欢先上代码😣

template<class KEY,class OTHER>
void AATree<KEY,OTHER>::insert(const SET<KEY,OTHER> &x,AANode *&t) {
    if(t == nullptr) {
        t = new AANode(x,nullptr,nullptr);
    }else if(x.KEY < t->data.KEY) {
        insert(x,t -> left);
    }else if(x.KEY > t -> data.KEY) {
        insert(x,t -> right);
    }else {
        return;
    }
    LL(t);
    RR(t);
}

template<class KEY,class OTHER>
void AATree<KEY,OTHER>::LL(AANode *&t) {
    if(t -> left != nullptr && t -> left->level == t -> level) {
        AANode *newRoot = t -> left;
        t -> left = newRoot -> right;
        newRoot -> right = t;
        t = newRoot;
    }
}

template<class KEY,class OTHER>
void AATree<KEY,OTHER>::RR(AANode *&t) {
    if(t -> right != nullptr && t -> right -> level == t -> level) {
        if(t -> right -> right != nullptr && t -> right -> right -> level == t -> level) {
            AANode *newRoot = t -> right;
            t -> right = newRoot -> left;
            newRoot -> left = t;
            t = newRoot;
            t -> level ++;
        }
    }
}

AA树对水平左链、连续水平右链的调整在某些《不好的时候》可能会发生多次，下面就是一个例子：（这例子真不错）

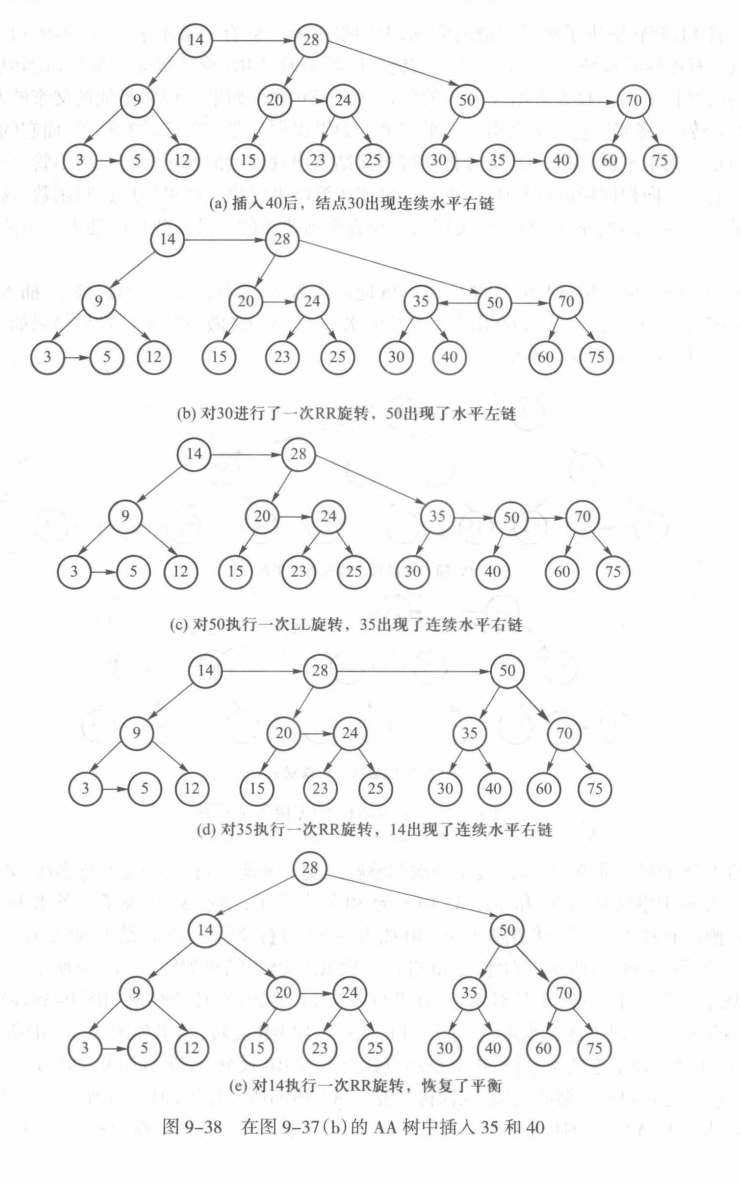
不管是什么问题，都可以通过在向根回溯的过程中反复应用 LL/RR 策略来解决。如果使用递归函数，这些回溯过程都是自动的。（就很好了😋）

AA树的删除操作

与BST相同，AA 树的删除也是归结为删除一个叶结点和删除一个只有一个儿子的结点。
AA 树的删除与 AVL 和红黑树一样，在结点被删除后要检查是否失去平衡。如果失去平衡，则需要调整。
我们分3种情况进行讨论：
（1） 删除结点是红结点，那么：无事发生
（2） 删除结点是黑结点，但有右孩子（这涵盖了一个条件：这个右孩子一定是红结点）。所以：直接将右孩子替换成被删结点，无事发生
（3）删除结点是黑结点，而且很不幸没有孩子。删除它将会影响平衡。

鉴于本人患有ADHD，所以还是先上代码😅😅😅

template<class KEY,class OTHER>
void AATree<KEY,OTHER>::remove(const KEY &k,AANode *&t) {
    if(t == nullptr) {
        return;
    }else if(k < t -> data.KEY) {
        remove(k,t -> left);
    }else if(k > t -> data.KEY) {
        remove(k,t -> right);
    }else {
        if(t -> left != nullptr && t -> right != nullptr) {
            AANode *tmp = t -> right;//找到下一个结点替代当前结点
            while(tmp -> left != nullptr) {
                tmp = tmp -> left;
            }
            t -> data = tmp -> data;
            remove(t -> data.KEY,t -> right);
        }else {
            //划归到那2种情况
            AANode *oldNode = t;
            if(t -> left != nullptr) {
                t = t -> left;
            }else {
                t = t -> right;
            }
            delete oldNode;
            return;
        }
    }
    //最后进行平衡的调整
    if(t -> left == nullptr || t -> right == nullptr) {
        t -> level = 1;
    }else {
        t -> level = min(t -> left -> level ,t -> right -> level) + 1;
    }
    if(t -> right != nullptr && t -> right -> level > t -> level) {
        t -> right -> level = t -> level;
    }
    LL(t);
    if(t -> right != nullptr) {
        LL(t -> right);
    }
    if(t -> right != nullptr && t -> right -> right != nullptr) {
        LL(t -> right -> right);
    }
    RR(t);
    if(t -> right != nullptr) {
        RR(t -> right);
    }
}

是不是关于调整的部分几乎完全看不懂？没事，因为我也一样😰😰😰
如果需要，对根结点执行 LL 旋转；如果需要，对根结点的右儿子执行 LL 旋转；如果需要，对根结点的右儿子的右儿子执行 LL 旋转；如果需要，对根结点执行 RR 旋转；如果需要，对根结点的右儿子执行RR旋转。
最坏情况下需要进行3次LL操作和2次RR操作
luogu上的一篇文章很详细地用图片展示了这一过程，指路👇：
AA树的删除操作

总结

AA树确实比AVL和RBT来的简洁不少。但是我个人认为AA树的删除操作可以通过具体的例子来说服我，但是依然从理论上来说并不能让我完全信服，我觉得我们有必要进行更深入的思考。