Algorithm Of DS——Fenwick Tree & Sparse Table

Before：2025.03.29，must be one of the best days in 2025.I can’t tell you why and I beg you don’t ask me why.I just hope to be like her and continue chasing after my dream,just like her and them.Whatever it takes.I just can’t help being excited about this wonderful meeting in Xuhui,Shanghai. Hope everything will be alright.

2025.03.29晚-徐家汇-上海

Algorithm of DS 2 Fenwick Tree and Sparse Table

Fenwick Tree 树状数组

一点点feeling：1~base在算法题里还是很香的😢

单点修改与区间查询

对于序列 $a_1,a_2,...,a_n$ 我们要支持一下操作：
（1）单点修改其中某个数 $a_i$
（2）查询 $\Sigma_{i = 1}^{k} a_i$

A problem we first met in the Chunking with a time complexity of O(n $\sqrt{n}$ ).（上机课上助教反复说过，可以用《线段树和树状数组解决》）所以要介绍的就是《树状数组》来解决这个经典问题。

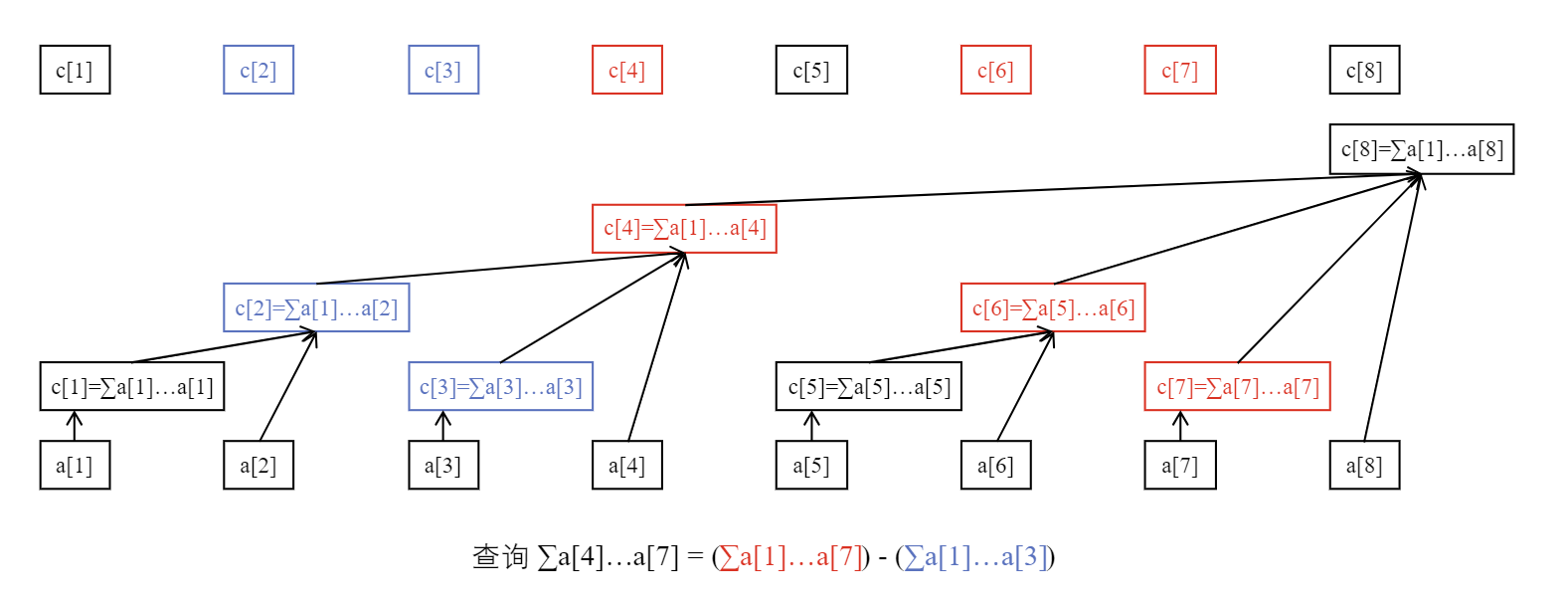
如下图所示，就展示了一个树状数组求解前缀和的很好的例子：

首先我们介绍树状数组中的预处理函数——lowbit函数！

1
2
3

int lowbit(int x){
    return x & (-x);//有时可能需要开成long long int
}

不难知道，这其实是x二进制表示下从右往左第一个出现1的位置。
每一个树状数组c[x]管辖的范围其实是：[x - lowbit(x) + 1,x]
为求得前缀和，每次回退lowbit(x)，得到新的x（新的起点）。如此往复，直到x = 0，代码实现如下：

int query(int x){
    int ans = 0;
    while(x > 0){
        ans += c[x];
        x -= lowbit(x);
    }
    return ans;
}

如果我需要得到区间[x,y]之间的和，则：

1	`return query(y) - query(x - 1);`

而对于更新操作，我们需要对第x位后包括x的所有树状数组的和进行加w的操作，相当于是一个逆过程：

void update(int x,int w){
    while(x <= n){
        c[x] += w;
        x += lowbit(x);
    }
}

区间修改和单点查询

似乎略有变化，实则并无变化，只是我们维护的树状数组c[x]是对于差分数组的。

1	`d[i] = a[i] - a[i-1];`

查询操作很简单，就是对差分数组求一个前缀和，函数实现一模一样。
如果要对某一区间[x,y]内的所有数进行一个 + w的操作，观察到，当i $\in$ [x + 1,y]时，d[i]不会发生变化，我们只需要修改首尾两处的d[i]即可，进行操作:

1 2	`update(x,w); update(y + 1,-w);`

区间修改与区间查询

又有了一些小变化，不妨列出来看一看：
$\Sigma_{i = 1}^{k} a_i$
= $\Sigma_{i = 1}^{k} \Sigma_{j = 1}^{i} d[i]$
= k * d[1] + (k - 1) * d[2] + … + 1 * d[k]
= (k + 1) $\Sigma_{i = 1}^{k} d[i]$ - $\Sigma_{i = 1}^{k} i * d[i]$

可见事实上我们只需要再多维护一个id[i]的树状数组就可以了(in fact 是这次小作业的某一题)，召唤术：区间修改与查找
hint：校外用户对不住了，ACMOJ只对sjtu内部开放😢😢

二维树状数组

Show me the Problem!
给定一个二维数组A，要求实现以下操作：
（1）单点修改A[x][y]
（2）单点查询A[x][y]
（3）子矩阵和查询：( $x_1$ , $y_1$ )为左上角，( $x_2$ , $y_2$ )为右下角
（4）子矩阵修改：( $x_1$ , $y_1$ )为左上角，( $x_2$ , $y_2$ )为右下角，所有元素加w

类似地建立树状数组c[x][y]表示以(x - lowbit(x) + 1,y - lowbit(y) + 1)为左上角，(x,y)为右下角的子矩阵的信息。
对于单点修改，思路大致不变，核心在于先固定一个然后修改另一个，使用循环嵌套：

void update(int x,int y,int w){
    for(int i = x;i <= n;i += lowbit(i)){
        for(int j = y;j <= m;j += lowbit(j)){
            c[i][j] += w;
        }
    }
}

对于子矩阵的查询，想法和一维也是一致的（若左上角为(1,1)）：

int query(int x,int y){
    int ans = 0;
    for(int i = x;i > 0;i -= lowbit(i)){
        for(int j = y;j > 0;j -= lowbit(j)){
            ans += c[i][j];
        }
    }
    return ans;
}

而如果是任意的子矩阵，可以通过容斥原理来解决：

1	`return query(x2,y2) - query(x1,y2) - query(x2,y1) + query(x1,y1);`

What about 区间修改和单点查询?
Redefine 差分数组：

1	`d[x][y] = a[x][y] - a[x - 1][y] - a[x][y - 1] + a[x - 1][y - 1];`

对差分数组构建一个树状数组，单点查询就被转变为了区间前缀和。

而对于区间修改，通过观察+想象（或者逻辑推演）可知：只需要对4个角进行修改，具体表现为：

update(x1,y1,w);
update(x1,y2 + 1,-w);
update(x2,y1 + 1,-w);
update(x2 + 1,y2 + 1,w);

Another 经典应用——树状数组求解逆序对数

核心在于:

int ans =  0;
for(int i = 1;i <= n;i ++){
    ans += query(maxN) - query(num[i]);
    update(num[i],1);
}

如果num[i]范围过大，可以采用离散化的方式防止RE😢😰
下面附上离散化的代码（de死我了，遇到了各种离谱的bug）：

#include<iostream>
using namespace std;
struct number {
    int Data;
    int pos;
};
void merge(const number*abegin,const number*aend,const number*bbegin,const number*bend,number*c) {
    while (abegin != aend && bbegin != bend) {
        if(abegin->Data < bbegin->Data) {
            *c = *abegin;
            abegin ++;
            c ++;
        }else {
            *c = *bbegin;
            bbegin ++;
            c ++;
        }
    }
    while(abegin != aend) {
        *c = *abegin;
        abegin ++;
        c ++;
    }
    while(bbegin != bend) {
        *c = *bbegin;
        bbegin ++;
        c ++;
    }
}
void merge_sort(number *a,int l,int r) {
    if(r - l <= 1) {
        return;
    }
    int mid = (l + r)/2;
    merge_sort(a,l,mid);
    merge_sort(a,mid,r);
    auto *tmp = new number[r - l + 1];
    merge(a + l,a + mid,a + mid,a + r,tmp);
    for(int i = l;i < r;i ++) {
        a[i] = tmp[i - l];
    }
    delete []tmp;
}
int c[500005];
int tem[500005];
number a[500005];
int n;
int lowbit(int x) {
    return x & (-x);
}
void update(int x,int w) {
    while(x <= n) {
        c[x] += w;
        x += lowbit(x);
    }
}
long long int query(int x) {
    long long int ans = 0;
    while(x > 0) {
        ans += c[x];
        x -= lowbit(x);
    }
    return ans;
}
int main() {
    long long int pairNum = 0;
    cin >> n;
    for(int i = 1;i <= n;i ++) {
        cin >> a[i].Data;
        a[i].pos = i;
    }
    merge_sort(a,1,n + 1);
    int id = 1;
    tem[a[1].pos] = 1;
    for(int i = 2;i <= n;i ++) {
        if(a[i].Data == a[i - 1].Data) {
            tem[a[i].pos] = id;
        }else {
            tem[a[i].pos] = ++ id;
        }
    }
    for(int i = 1;i <= n;i ++) {
        pairNum += query(id) - query(tem[i]);
        update(tem[i],1);
    }
    cout << pairNum;
}

Sparse Table ST表

ST 表（Sparse Table，稀疏表）是用于解决可重复贡献问题的数据结构。

RMQ问题

Problem First😢😢😢：
给定n个数，m次询问，对于每个询问，回答区间[l,r]中的最大值。

我们发现区间最大值是一个具有「可重复贡献」性质的问题。即使用来求解的预处理区间有重叠部分，只要这些区间的并是所求的区间，最终计算出的答案就是正确的。我们能使用至多两个预处理过的区间来覆盖询问区间，也就是说询问时的时间复杂度可以被降至O(1)，在处理有大量询问的题目时十分有效。

令f(i,j)表示区间[i,i + $2^j$ - 1]区间上的最大值。对于每个询问，我们把它分为[l,l + $2^s$ - 1]和[r - $2^s$ + 1,r]，其中s = $log_2{r - l + 1}$ 。

鉴于log操作计算量较大（double），我们考虑用一个函数手写一下：（和OiWiki上的想法不太一样，但感觉能用）

int log(int x){
    int i = -1;
    while(x){
        x /= 2;
        i ++;
    }
    return i;
}

首先是预处理：

1
2
3

for(int i = 1;i <= n;i ++){
    cin >> f[i][0];
}

接着就是倍增处理了：

for(int i = 1;i <= 21;i ++){ //如果数据是1e6级的，那么21就查不多了，甚至不用调用函数再算一下
    for(int j = 1;i + (1 << j) - 1 <= n;j ++){
        f[i][j] = std::max(f[i][j - 1],f[i + (1 << (j - 1))][j - 1]);
    }
}

而当查询时，就更简单了：

1 2	`int s = log(r - l + 1); cout << std::max(f[i][s],f[r - (1 << s) + 1][s]);`

超级经典问题——与众不同！

指路：与众不同
思路：记f(i)表示以第i个位置为结尾的最长完美序列的左端点位置，容易发现f(i)是不降的对于一个[l,r]的询问，我们将区间中的点分成左右两部分，左边的点满足f(i)<L,右边的点满足f(i)≥L, 对于左边的点我们可以直接算出答案，对于右边的点我们可以用st表区间询问求得答案。

上代码：

#include <iostream>
using namespace std;
int n,m;
int LastExist[2000005];
int position[200005];
int f[200005][20];//ST表
int LOG(int x) {
    int i = - 1;
    while(x) {
        x /= 2;
        i ++;
    }
    return i;
}
int main() {
    std::ios::sync_with_stdio(false);
    cin.tie(0); 
    cout.tie(0);
    cin >> n >> m;
    for(int i = 1;i <= n;i ++) {
        int x;
        cin >> x;
        x += 1000001;
        position[i] = max(position[i - 1],LastExist[x] + 1);
        LastExist[x] = i;
    }
    int l,r;
    //ST表初始化
    for(int i = 1;i <= n;i ++) {
        f[i][0] = i - position[i] + 1;
    }
    for(int j = 1;j <= 21;j ++) {
        for(int k = 1;k + (1 <<j) - 1 <= n ;k ++) {
            f[k][j] = max(f[k][j - 1],f[k + (1<<(j - 1))][j - 1]);
        }
    }
    for(int i = 0;i < m;i ++) {
        cin >> l >> r;
        l ++;
        r ++;
        int maxLength = -1;
        int newstart = - 1;
        for(int j = l;j <= r;j ++) {
            if(position[j] < l) {
                maxLength = j - l + 1;
            }else {
                newstart = j;
                break;
            }
        }
        if(newstart ==  - 1) {
            cout << maxLength << endl;
            continue;
        }
        int s = LOG(r - newstart + 1);
        int another = max(f[newstart][s],f[r - (1 << s) + 1][s]);
        if(another > maxLength) {
            maxLength = another;
        }
        cout << maxLength << endl;
    }
    return 0;
}

Reference

Algorithms

#Data Structure #Algorithm #Fenwick Tree #Sparse Table #RMQ

Algorithm Of DS——Fenwick Tree & Sparse Table

http://example.com/2025/04/05/AlgorithmOfDS2/

Author

Yihan Zhu

Posted on

April 5, 2025

Updated on

April 6, 2025

Licensed under

数据结构7 Previous

Data Structure 19 B Tree & B+ Tree Next