数据结构 8 Sorting

Before:第10章排序并未提前进行学习，所以会结合翁阿姨上课的笔记和课后学习，内容比较完善

数据结构 8 排序

所谓排序就是把集合中的数据元素按照它们的关键字的非递减或非递增序排成一个序列。

插入排序

首先将由第一个数据元素组成的序列看成是有序的，然后将剩余的n-1个元素依次插入到前面的已排好序的子序列中去，使得每次插入后的子序列也是有序的。

插入排序又分为：

直接插入排序

暴力插入，复杂度O($N^2$)

折半插入排序

利用二分查找法，快速地找到a[j]的插入位置，但这只会减少比较次数，并不会改变元素的移动，所以复杂度还是O($N^2$)

希尔排序 缩小增量排序法

1.将待排序序列分为若干子序列（每个子序列的元素在原始数组中间距相同）；
2.对这些子序列进行插入排序；
3.减小每个子序列中元素之间的间距，重复上述过程直至间距减少为 1。

template<class KEY,class OTHER>
void shell_sort(SET<KEY,OTHER>a[],int size){
    int step;
    int i,j;
    SET<KEY,OTHER> tmp;
    for(step = size/2;step > 0;step /= 2){
        //希尔增量
        for(i = step;i < size;i ++){
            tmp = a[i];
            for(j = i - step;a[j].KEY > tmp.KEY;j -= step){
                a[j + step] = a[j];
            }
            a[j + step] = tmp;
        }
    }
}

选择排序

首先，从n个元素中选出关键字最小的元素。再从剩下的(n-1)个元素中选出关键字最小的元素，依次类推，每次从剩下的元素序列中挑出关键字最小的元素，直至序列中最后只剩下一个元素为止。

直接选择排序

暴力，复杂度O($N^2$)(不能存在最好最坏情况，必须全做)

堆排序 HeapSort！

建堆复杂度：O(N) （we’ve already proved this in priority_queue）
出队操作：O(logN)
总时间复杂度：n次出队O(nlogn)

交换排序

冒泡排序（数据本就比较有序）

从头到尾比较相邻的两个元素，将小的换到前面，大的换到后面。经过了从头到尾的一趟比较，就把最大的元素交换到了最后一个位置。这个过程称为一趟起泡。

快速排序（数据比较杂乱）

在待排序的序列中选择一个数据元素，以该元素为标准，将所有数据元素分为两组，第一组的元素均小于或等于标准元素，第二组的数据元素均大于标准元素。第一组的元素放在数组的前面部分，第二组的数据元素放在数组的后面部分，标准元素放在中间。这个位置就是标准元素的最终位置。这称为一趟划分。然后对分成的两组数据重复上述过程，直到所有的元素都在适当的位置为止。

我觉得我们有必要回忆一下快排是怎么写的😅

template<class KEY,class OTHER>
int divide(SET<KEY,OTHER> a[],int low,int high){
    SET<KEY,OTHER> tmp = a[low];
    do{
        while(low < high && a[high].KEY >= tmp.KEY){
            high --;
        }
        if(low < high){
            a[low] = a[high];
            ++ low;
        }
        while(low < high && a[low].KEY <= tmp.KEY){
            low ++;
        }
        if(low < high){
            a[high] = a[low];
            high --;
        }
    }while(low != high);
    a[low] = tmp;
    return low;
} 

template<class KEY,class OTHER>
void quick_sort(SET<KEY,OTHER> a[],int low,int high){
    int mid;
    if(low >= high){
        return;
    }
    mid = divide(a,low,high);
    quick_sort(a,low,mid - 1);
    quick_sort(a,mid + 1,high);
}

template<class KEY,class OTHER>
void quicksort(SET<KEY,OTHER> a[],int size){
    quick_sort(a,0,size - 1);
}

快速排序的性能分析：（递归函数时间性能分析）
T(N) = T(i) + T(N - i - 1) + c(N)
T(0) = T(1) = 1

快排的最坏情况：选择的元素最大or最小
T(N) = T(N - 1) + c(N)
T(N - 1) = T(N - 2) + c(N - 1)
…
T(2) = T(1) + c(2)

T(N) = T(1) + c(2 + 3 + … + N) = O($N^2$)

快排的最好情况：分成等长的2段
T(N) = 2T(N/2) + cN
将等式两边同时除N，可得：
T(N)/N = T(N/2)/(N/2) + c
T(N/2)/(N/2) = T(N/4)/(N/4) + c
…
T(2)/2 = T(1)/1 + c

即：T(N) = cnlogn + n = O(nlogn)

平均情况分析：
T(N) = 2(T(0) + … + T(N - 1))/N + cN
经过数列计算可得：T(N) = O(nlogn)

归并排序

很熟悉了，直接贴板子

void merge(const int *aBegin, const int *aEnd, const int *bBegin,
           const int *bEnd, int *c) {
  while (aBegin != aEnd && bBegin != bEnd) {
    if (*bBegin < *aBegin) {
      *c = *bBegin;
      ++bBegin;
    } else {
      *c = *aBegin;
      ++aBegin;
    }
    ++c;
  }
  for (; aBegin != aEnd; ++aBegin, ++c) *c = *aBegin;
  for (; bBegin != bEnd; ++bBegin, ++c) *c = *bBegin;
}

void merge_sort(int *a, int l, int r) {
  if (r - l <= 1) return;
  // 分解
  int mid = l + ((r - l) >> 1);
  merge_sort(a, l, mid), merge_sort(a, mid, r);
  // 合并
  int tmp[1024] = {};  // 请结合实际情况设置 tmp 数组的长度（与 a 相同），或使用
                       // vector；先将合并的结果放在 tmp 里，再返回到数组 a
  merge(a + l, a + mid, a + mid, a + r, tmp + l);  // pointer-style merge
  for (int i = l; i < r; ++i) a[i] = tmp[i];
}

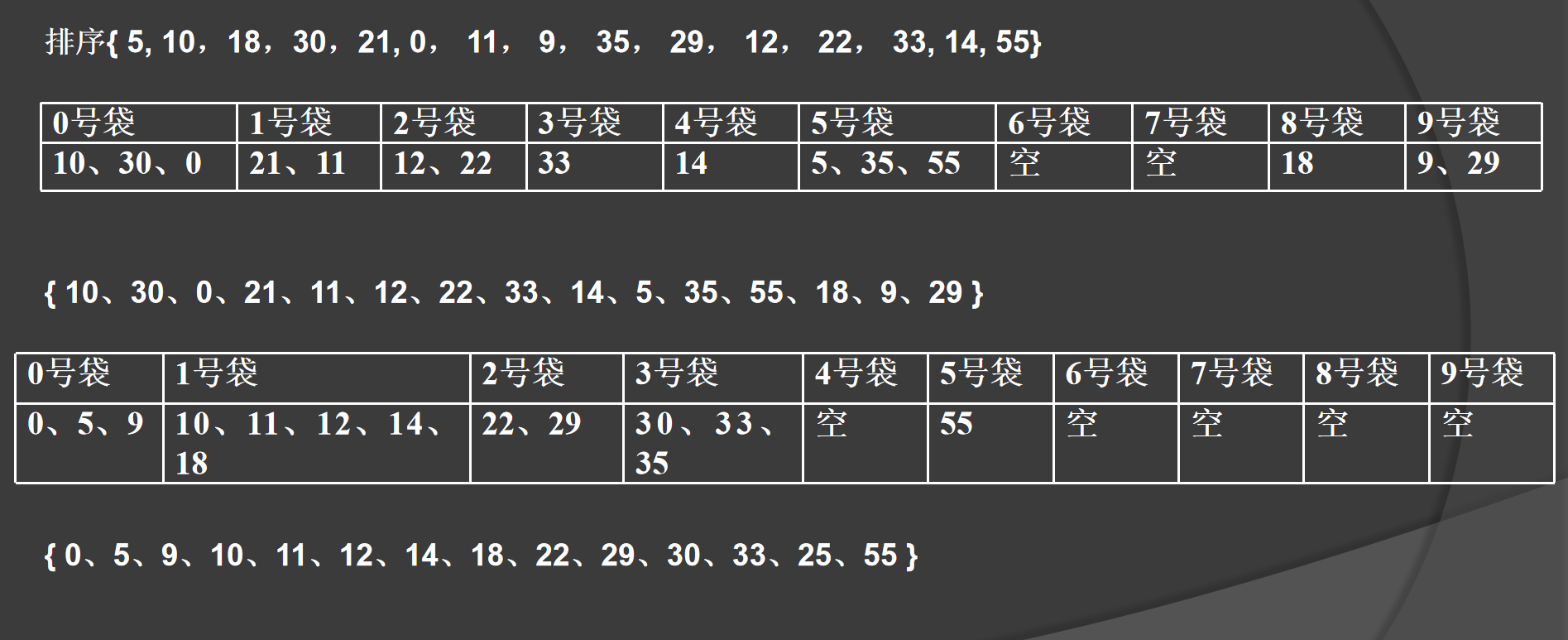
基数排序

感觉基数排序很有意思：以排序十进制非负整数为例，可设置10个口袋：

• 首先将元素按个位数分别放入十个口袋，然后将每个口袋中的元素倒出来
• 按元素的十位数分别放入十个口袋。然后把它们倒出来
• 再按百位数分配
• 到最后一次倒出来时，元素就已经排好了序

Example:

我们可以用单链表来实现：

template<class OTHER>
struct node{
    SET<int,OTHER> data;
    node *next;
    node(){
        next = nullptr;
    }
    node(SET<int,OTHER> d):data(d){
        next = nullptr;
    }
}

template<class OTHER>
void bucketSort(node<OTHER>* &p){
    node<OTHER> *bucket[10];
    node<OTHER> *last[10];
    node<OTHER> *tail;
    node<OTHER> *tmp = p;
    int maxNum = -1;
    while(tmp != nullptr){
        if(tmp -> data.key > maxNum){
            maxNum = tmp -> data.key;
        }
    }
    int len = 0;
    while(maxNum > 0){
        maxNum /= 10;
        ++ len;
    }
    int base = 1;
    for(int i = 1;i <= len;i ++){
        for(int j = 0;j <= 9;j ++){
            bucket[j] = nullptr;
            last[j] = nullptr;
        }
        while(p != nullptr){
            int k = (p -> data.key / base) % 10;
            if(bucket[k] != nullptr){
                last[k] -> next = p;
                last[k] = last[k] -> next;
            }else{
                bucket[k] = p;
                last[k] = p;
            }
        }
        p = nullptr;//置空链表头
        for(int j = 0;j <= 9;j ++){
            if(bucket[j] != nullptr){
                if(p == nullptr){
                    p = bucket[j];
                }else{
                    tail -> next = last[j];
                }
                tail = last[j];
            }
        }
        base *= 10;
        tail -> next = nullptr;//！！别忘了置空！！
    }
}

Conclusion

感觉JaneZ现在是排序大师了bushi😄😄😄