Before：久违的数理逻辑课！上了7节课终于觉得有点入门了，还是挺有意思的。周四下午闪击南京，周五下午又闪击回来。虽然只有1天，但很开心在这短短的20个小时内帮助了不少人（都是无意间）。我要永远做个善良的人！

Mathematical Logic 7 Completeness 1

我们继续完备性的证明！
我们知道，要证明一阶逻辑的完备性，我们只需要证明：

Given a consisitent $\Phi$,it suffices to construct a term model $\mathfrak{I}^{\Phi}$ = ($\mathfrak{T}^{\Phi},\mathfrak{\beta}^{\Phi}$) such that:
$\mathfrak{I}^{\Phi}$ $\models$ $\varphi$ \iff $\Phi$ $\vdash$ $\varphi$.

昨晚室友问我为了体现完备性，就是要证明$\Phi$ $\models$ $\varphi$, $\Phi$ $\models$ $\varphi$ 难道不是在说对于任何一个$\Phi$ 上的模型，都能使$\varphi$为真吗？但是这里不是只找了一个模型吗？我想这应该是由于Henkin’s Term Model的特殊性，但这个留到后几节课再讨论了。

Henkin’s Term Model Recall 模型回顾

首先引入等价类的概念：
Let $ t_1,t_2 $ $\in$ $T^S$.Then $ t_1 $ ~ $ t_2 $ if $\Phi$ $\vdash$ $t_1\equiv t_2$.

For every t $\in$ $T^S$ we define:
$\overline{t}$ := {t’ $\in$ $T^S$ |t’ ~ t}

Definition
The term structure for (\Phi), denoted by (\mathfrak{I}^{\Phi}), is defined as follows.

1. Universe:
   $T^{\Phi} := \{\overline{t} \mid t \in T^S\}.$

2. Relation symbols:
   For every \(n\)-ary relation symbol \(R \in S\), and \(\overline{t_1}, \ldots, \overline{t_n} \in T^{\Phi}\),
   $(\overline{t_1}, \ldots, \overline{t_n}) \in R^{\mathfrak{I}^{\Phi}} \quad \text{if} \quad \Phi \vdash R t_1 \ldots t_n.$

3. Function symbols:
   For every \(n\)-ary function symbol \(f \in S\), and \(\overline{t_1}, \ldots, \overline{t_n} \in T^{\Phi}\),
   $f^{\mathfrak{I}^{\Phi}} (\overline{t_1}, \ldots, \overline{t_n}) := f \overline{t_1} \cdots t_n.$

4. Constants:
   For every constant \(c \in S\),
   $c^{\mathfrak{I}^{\Phi}} := \overline{c}.$

For every variable $v_i$,we let:
\mathfrak{\beta}^{\Phi}\(v_i\) := $\overline{v_i}$

对于原子公式成立 atomic $\varphi$

Lemma 5

(i) For any \( t \in T^S \),
$\mathfrak{I}^\Phi(t) = \bar{t}.$

(ii) For every atomic \(\varphi\),
\mathfrak{I}^\Phi \models \varphi \iff \Phi \vdash \varphi.

(i)的证明，我们对项t进行归纳：

• t = $v_i$ is a variable
• t = c is a constant
• t = f$t_1...t_n$

根据定义可证

(ii)的证明，对2个原子公式进行分类讨论：
$\mathfrak{I}^\Phi \models t_1 \equiv t_2$
$\mathfrak{I}^\Phi \models Rt_1...t_n$
利用(i)中所证，可证

Consistent,Negation Complete,Contains Witness

Lemma 8

先看一个引理：

Lemma 8

Let (\varphi) be an (S)-formula and (x_1, \ldots, x_n) pairwise distinct variables. Then

(i)

$\mathfrak{I}^\Phi \models \exists x_1 \ldots \exists x_n \varphi$
if and only if there are (S)-terms (t_1, \ldots, t_n) such that
$\mathfrak{I}^\Phi \models \varphi \frac{t_1 \ldots t_n}{x_1 \ldots x_n}.$

(ii)

$\mathfrak{I}^\Phi \models \forall x_1 \ldots \forall x_n \varphi$
if and only if for all (S)-terms (t_1, \ldots, t_n) we have
$\mathfrak{I}^\Phi \models \varphi \frac{t_1 \ldots t_n}{x_1 \ldots x_n}.$

由替换引理等可证

Consistent

Definition
$\Phi$ is consistent if there is no $\varphi$ such that both $\Phi$ ⊢ $\varphi$ and $\Phi$ ⊢ $\neg$$\varphi$. Otherwise,$\Phi$ is inconsistent.

Negation Complete

Definition
A set (\Phi) is negation complete if for every (S)-formula (\varphi):
$\Phi \vdash \varphi \text{ or } \Phi \vdash \neg \varphi.$

通俗的说，就是如果$\Phi$ 证不出来$\varphi$，那就一定能证出来$\neg \varphi$；证不出来$\neg \varphi$，那就一定能证出来$\varphi$

Contains Witness

Definition

🔍 A set $\Phi$ contains witnesses if for every $\varphi \in L^S$ and every variable $x$, there exists a term $t \in T^S$ such that:

$\Phi \vdash \left( \exists x \varphi \to \varphi \frac{t}{x} \right).$

Henkin’s Theorem Proof

First,还是先来证明一个引理：

Lemma 9

Assume that $\Phi$ is consistent, negation complete, and contains witnesses. Then for all $S$-formulas $\varphi$ and $\psi$:

(i)
$\Phi \vdash \varphi$ if and only if \Phi \not\vdash \neg \varphi.

(ii)
$\Phi \vdash (\varphi \vee \psi)$ if and only if $\Phi \vdash \varphi$ or $\Phi \vdash \psi$.

(iii)
$\Phi \vdash \exists x \varphi$ if and only if there is a term $t \in T^S$ such that $\Phi \vdash \varphi \frac{t}{x}$.

(i)向右通过consistent定义说明，向左通过negation complete定义说明
(ii)向左利用V-intro by succedent证明，向右证明如下：
Assume that $\Phi \vdash \neg \varphi$
Proof Steps:

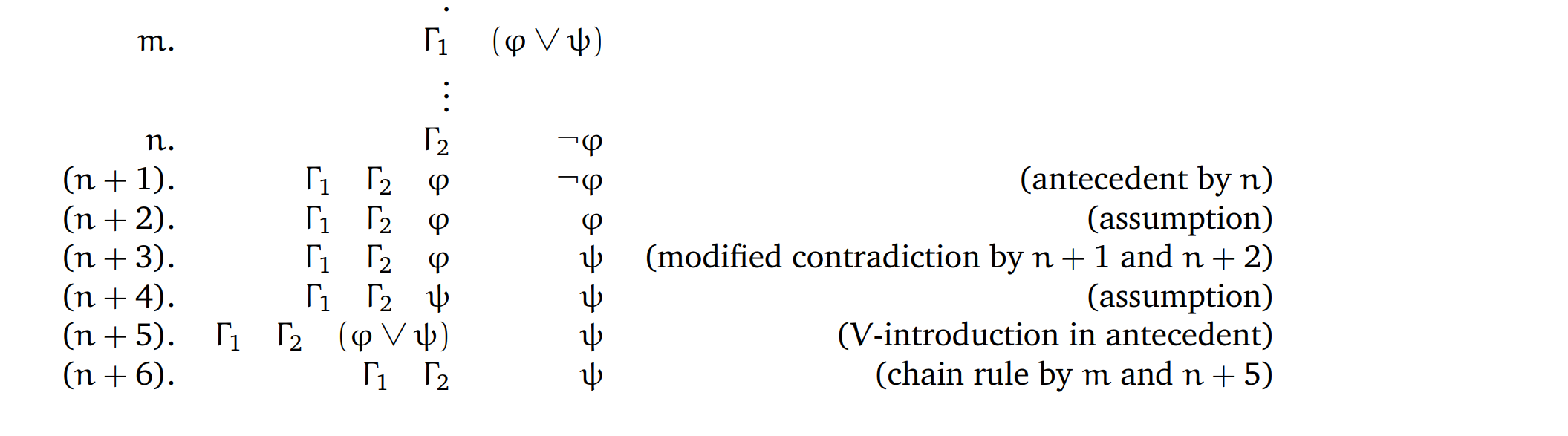
(iii)向右可通过Modus ponens证明，向左可通过\exist-intro in succedent证明

Henkin’s Theorem

由引理证明起来还是比较显然的：

注意，这里对公式的归纳是对公式的connective rank归纳，保证要证的公式都更长：
Rank Definition:
rk(\varphi) := \begin{cases} 0 & \text{if } \varphi \text{ is atomic,} \ 1 + rk(\psi) & \text{if } \varphi = \neg\psi, \ 1 + rk(\psi_1) + rk(\psi_2) & \text{if } \varphi = (\psi_1 \lor \psi_2), \ 1 + rk(\psi) & \text{if } \varphi = \exists x \psi. \end{cases}